An attempt to consider either variable always as the input or independent variable leads to severe numerical stiffness problems. In addition, the system structure changes during clutching. It is, therefore, desirable to have a systematic and logical procedure for the modelling process.

One such systematic procedure is to be found in the bond graph method. In this paper is therefore presented a bond graph representation of the clutching process in which the system structure remains constant, numerical stiffness problems are easily handled, and the jump condition after clutching is taken care of automatically. The proposed method is used to simulate an actual propulsion system, and the results are compared to measurements. The influence of certain parameters on the transient performance is also exemplified.

　

2. BOND GRAPHS

　

Bond graphs have been developed as an ambitious scheme to aid in the mathematical modelling and subsequent analysis and simulation of dynamic physical systems that occur in engineering. Breedveld et al. [1] has compiled a bond graph bibliography which contains numerous books, articles and papers from a wide variety of application areas.

Bond graphs are a unified graphical notation for the representation of physical systems [2], [3]. The basic concept is that power is the fundamental constraint in a physical system and is the one variable that is common to the whole system. Bond graphs consist of letters and numbers representing the components connected by lines or bonds standing for power interactions.

The bond is considered to conduct power between the ports instantaneously and without loss. Each bond has an effort, e, and flow, f, signal and in true bond graphs the product of the two signals is the instantaneous power between system A and B shown below.

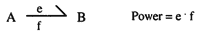
The half arrow shows the direction in which the positive power is flowing. Two other types of variables that are important are momentum, p, and displacement, q, in generalized notation. Momentum is defined as the time integral of an effort and the displacement variable is the time integral of a flow variable. Momentum and displacement variables can be used to represent system energy and thus state variables.

Using the classification of power and energy variables presented previously, it turns out that only nine basic types of multi-port elements are required in order to represent models in a variety of energy domains. These multi-ports function as components of subsystem and system models. They are, in many cases, idealized mathematical versions of real components, and in other cases they are used to model physical effects. The nine basic multi-ports are classified in Table 1, according to the way they process energy. Roughly speaking, these elements account for energy supply, dissipation, storage and transduction from one mode to another (conversion of energy from one form to another).

　

Table 1. Basic bond graph elements.

　

Using these basic elements, a graphical model can be constructed of a system. It is a remarkable fact that models based on apparently diverse branches of engineering science all can be expressed using the notation of bond graphs. This allows one to study the structure of a system model. The nature of the parts of the model and the manner in which the parts interact can be made evident in a graphical format.

Using bond graphs, the differential equations can be constructed in an algorithm manner from the graph. That is the graph is perfectly equivalent to the differential equations of the form

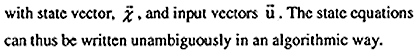
However, before the equations can be written from the bond graph, causal information must be added to the graph. Causality means obtaining an explicit indication of which variables for an element is to be considered independent and which are to be considered dependent. Said another way, which are the inputs and which are the output variables. The problem of assigning a particular causality to a system model is related directly to the manner in which the system can be simulated, or the manner in which the system equations can be written without difficulty.

BACK　　　CONTENTS　　　NEXT