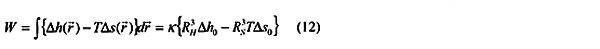H denote Henry's constant. For temperatures between 0 and 100 degree Celsius it is well represented by the empirical temperature function (Austgen et.al. (1991)):
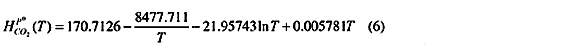
The ideal gas chemical potential for a spherical model of carbon dioxide is trivially obtained as described in any standard textbook on physical chemistry and will not be repeated here. Similarly for the ideal gas of TIP4P, which in addition has three well-defined rotational momentums.
A hydrate that forms on the interface between pure carbon dioxide, like in the situation of a carbon dioxide lake at large depths or on the surface of a carbon dioxide plume will result in a diffusion controlled growth rate that depends on the diffusion of water and hydrate formers through the hydrate film, mainly through pores and imperfections. One extreme approximation is to consider the hydrate film to completely close the interface. Within this hypothetic picture direct insertion of the chemical potential for carbon dioxide at 300 bar and 3 degrees Celsius into equation (3) and requiring that the chemical potential of water in hydrate (equation (2)) has to be equal to that of water in the seawater (equation (1)) gives a sub-cooling of the hydrate in the order of 23 degrees Celsius. On the other side of the hydrate film we also require that both water and carbon dioxide have to be in equilibrium between hydrate and liquid phase.
In fig. 1 we plot the limiting seawater concentrations of carbon dioxide that is necessary in order to give equilibrium between hydrate and seawater containing carbon dioxide. It is seen that for instance at 300 bar and 3 degree Celsius the necessary concentration of carbon dioxide in order to reach equilibrium with hydrate is about 30% of the saturation concentration.
IV. KINETIC THEORY
Classical nucleation theories are based on the assumption that the thermodynamic properties of the nuclei of the new phases are uniform throughout the volume of these nuclei. It is reasonable, according to Gibb's phase rule and the first and second law's of thermodynamics, that chemical potentials of individual components are constant throughout the co-existing phases. Partial molar enthalpies, entropies and volumes on the surface of the nuclei will however be different. In statistical mechanics this follows trivially from the grand canonical ensemble. The consequence of not taken into consideration any difference in thermodynamic properties between the bulk nuclei and the surface of these nuclei is that the driving forces for nucleation are not correct. The effective range of change in thermodynamic properties will depend on the actual phases involved. For a condensation from gas to liquid it will typically be in the order of 2 - 4 molecular diameters (the effective range of the direct interactions) for non-polar systems. This range will change depending on system and actual phase transition considered. For small nuclei the corresponding volume of property changes will constitute a significant portion of the nuclei volume. Neglecting these effects will therefore inevitably lead to incorrect nucleation rates, an issue that also has been demonstrated by Granasy (1996b) through comparison's between classical nucleation theories and DIT theory. For the systems compared the DIT theory is in striking agreement with experiments whereas classical nucleation theories may even fail by orders of magnitude in nucleation rates. Kvamme (2000) extended the DIT theory to multi-component systems. In the following we will use the notation MDIT for this extended version of the theory. The work term in the MDIT theory may be written as: