3.4 補強板
補強板の座屈応力、横荷重を受ける場合のたわみおよび応力の計算は平板の場合より複雑になるが、種々の設計図表があるので、必要に応じてそれらを利用するとよい。(たとえば関西造船協会編造船設計便覧、海文堂を参照のこと。)
3.5 柱の座屈応力
長さlの柱が圧縮荷重を受けるときの座屈応力を計算する公式として次のものがある。
(1) オイラーの公式
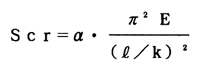
ただし、αは柱の両端の支え方によって決まる係数で、
(a) 両端支持 α=1
(b) 一端自由他端固定 α=1/4
(c) 一端支持他端固定 α=2
(d) 両端固定 α=4
Eは材料のヤング係数、l/kは細長比である。
上式で示されるように、細長比が大きい程座屈応力は低下することになる。細長比に対して座屈応力を表した曲線(第15図参照)をオイラー曲線と呼ぶ。
(2) ゴールドン・ランキンの公式
オイラー曲線では、細長比が大きいときは座屈応力は低く、その材料の弾性範囲内にあるが、細長比が小さくなるにつれて、オイラー曲線によれば座屈応力はいくらでも上昇しうることになる。しかし、圧縮応力が降伏応力に達すれば当然破損を生ずるから、短柱の強度は降伏応力で決められることになり、第15図の降伏応力を示す水平線が破損応力の最大値を与えることになる。この直線とオイラー曲線との交点付近、すなわち長柱から短柱に移る細長比に対する座屈応力は、これらの線よりも低いことが実験的に求められている。したがって、このような中位の細長比に対する柱の座屈強度を与える実験式が数多く提案されているが、よく使われるものとして次のゴールドン・ランキンの公式がある。(第15図参照)