The parameters adjusted in these runs thus formed a reduced state space from the total model state space, which speeds calculation of the sensitivities.
The quasi-geostrophic relations reduce the number of unknowns. Instead of estimating temperature, salinity, density, and velocity separately while applying diagnostic constraints (such as geostrophy and non-divergence), the only unknown is streamfunction, from which density, velocity, and temperature and salinity are derived by assuming geostrophic balance and adiabatic motion. Observations of density, velocity, surface height, etc., are linearly related to the streamfunction field by the diagnostic relations of quasigeostrophic theory. The streamfunction expansion in vertical eigenmodes is best in a region with weak horizontal variation in the mean state and topography.
The spectral expansion used for the horizontal parameterization of the streamfunction satisfies doubly periodic boundary conditions, which cannot be altered without changing the model basis functions. For this model, the only option is to place the boundaries far from the region with data. In the examples considered here the periodicity length (model domain) was twice as large as the horizontal extents of the observations, to reduce the impact of the periodicity on the estimates. To the extent that the model is nonlinear, the dynamical evolution is incorrect in regions where the field is poorly determined, but the error estimates from the estimation contain this information. The need to prevent significant information from propagating out one side of the box and into the other limits the maximum time over which the model fit can be run realistically.
SOLUTION METHOD
The first step in estimating initializations was to compute the quantative relations between the observations and the unknowns, called the‘forward problem’. For the direct temperature measurements, this is just a matter of evaluating the basis functions at the location of the datum. For the acoustic travel times, a numerical raytrace program was used to trace rays through the three-dimensional reference sound speed field (computed from the modified Levitus climatology). The travel times calculated from the raytrace were subtracted from the observations to produce travel time perturbations (measured minus predicted), which were corrected for the motion of the instruments, which were tracked to about 1 m accuracy in all dimensions. The corrected travel time perturbations had variability due to ocean changes of about 0.05 seconds rms, compared to internal wave“noise”of about 0.005 seconds rms (after daily averaging). The rays show an even distribution of upper and lower turning depths, providing good vertical resolution. (Figure 2) The dependence of the travel time perturbations on the model parameters was calculated by integrating the model basis functions (converted to sound speed) along each ray path.
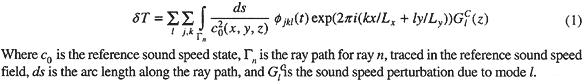
Measurements only exist at scattered space-time points within the region of interest, and the goal of the inverse procedure is to produce a field which obeys the model dynamics and agrees with the data to within an acceptable margin of error. The model parameters that best fit the data are determined by iterating a linearized, time-dependent least-squares inverse.