参考資料5.1-2

制約水域における航過距離と離隔距離に関する操船者意識のモデル化

(平成6年　日本航海学会論文集　井上欣三、宇佐美茂、柴田登紀子)

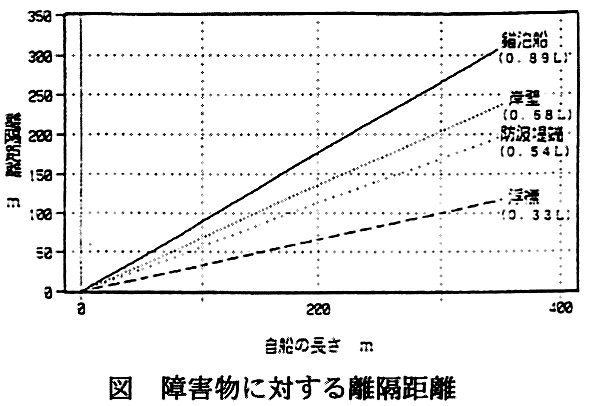
離隔距離モデル

離隔距離についても航過距離の場合と同様の方法により、自船の長さをベースに確保したい離隔距離の大きさをプロットした図を作成したうえで、これを直線により回帰し、モデル化を行った。図はそれぞれの障害物の種類ごとに回帰した結果を示している。それぞれの回帰式は次式により表される。

これによると同じ港内にある障害物であっても、接触した場合の互いの損害の大きさや振れ回り・移動の状況、航過に要する時間などを考慮し、これらがシビアであるほど離隔距離を大きく取るという傾向が現れている。

D(浮　　標)＝0.33・L₀

D(防波堤端)＝0.54・L₀

D(岸　　壁)＝0.68・L₀

D(錨 泊 船)＝0.89・L₀

ただし、D：障害物に対する離隔距離[m]

　

「制約水域における航過距離と離隔距離に関する操船者意識のモデル化」による検討

(平成6年度　本州四国連絡橋航行安全調査報告書　-航行安全調査その1-　資料編)

「制約水域における航過距離と離隔距離に関する操船者意識のモデル化」(井上欣三他、日本航海学会)によると、船舶が行き会う場合の必要可航幅は、満足率80%で求めると次式で表される。

航過距離(十分)p=1/2{(0.012・Lt+1.096)・L₀-b₀}×2

p：十分航過左舷距離

L₀：自船の長さ(m)

L_t：他船の長さ(m)

b₀：自船の幅(m)

離隔距離D(防波堤端)=0.54・L₀×2

D：障害物に対する離隔距離

可航幅=航過距離p＋離隔距離D₀+離隔距離D_t＋船幅b₀+船幅b_t

D₀：自船の離隔距離

D_t：他船の離隔距離

b_t：他船の幅(m)

上記述より、例えば東水道の通航実態から観測された最大通航船型65m(幅10m)が自航台船で二分された広い方の水域で対面通航する場合を計算すると、

p=(0.012×65+1.096)×65-10=111.94m

D₀：0.54×65×2=70.2m

D_t：0.54×65×2=70.2m

b₀：10m

b_t：10m

可航幅=p＋D₀+D_t+b₀+b_t

=111.94+70.2+70.2+10+10=272.32m

前ページ　　　目次へ　　　次ページ