面温度（K）を示す。

多くの場合、熱伝達率はヌセルト数（Nu；Nusselt number）から求めることができる 7）。例として、受熱体を平板とすれば流れに平行に置かれた場合、強制熱伝達率はペクレ数（Peclet Number）を用いて次式で与えられおり、Nuは流速に比例することとなる。

ここで、l（m）は平板の長さ、U（mS −1）は風速、a（m 2S −1）は固体の温度伝導率を示す。Cnは空気の場合0.075、燃焼ガスの場合0.077である。

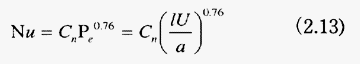
本報告では、高温ガスは周囲空気と混合によって、温度が低下することも考慮して、温度低下が火源からの距離に反比例するものと仮定する。風の影響は、風向によって異るためこれをδ関数を用いて、熱源から受熱体に向かって風が吹いている場合を1、それ以外の場合は影響が無いとして0として表すものとする。またガス温度は火源寸法（d）にも依存するから次式が得られる。

ここで、Dは定数とする。

以上整理して、制限条件（2.1）式は次式で表すことができる。

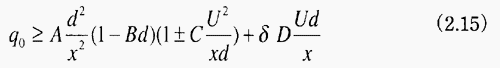
定数A,B,C,Dは（2.4）、（2.8）、（2.10）、（2.14）の式で与えられる。

2.2.5 数値計算例

数値を算出するには、各定数を実験データから決めなければならない。ここでは、（2.5）、（2.6）に関する実験値から試算した。

図2.2.5は熱放射強度と距離の関係を示す。ポイントデータとして実験値 5）Rf＝40,845Wm −2（カフジ原油）,d＝10m,x＝32.1m,qrad＝1,246Wm −2をもとに計算した熱放射強度と火源からの無次元距離との関係を示したもので、火炎の極めて近傍では19KWm −2に達していることがわかる。

前ページ　　　目次へ　　　次ページ