対して置かれていたとする。面積Aの平面に電波が垂直に入射したときのこの平面のレーダー断面積σは、
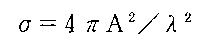
であることが知られている。いま、A = 30×30(cm2乗)であるので、このσはσ≒1.13×10の6乗(cm6乗)となり、これは半径6mの球の断面積に相当する。その代わり、この平面がちょっとでも傾けばσ = 0 となる。ただし、これは電波を幾何光学的に考えたときで、実際はこのような平板は若干の指向性をもって電波を反射するので、少しぐらい傾いてもレーダーの方向にその電波を反射する性質を持っている。このように、ある特定の反射体はその面積と比べて非常に大きなレーダー断面積を持つことが可能であり、次節で扱うレーダー反射器はこの性質を利用したものと考えればよい。
一般に大型船のような複雑な構造をもった物体は球体ほど均一ではないが、四周に電波を反射する性質を持っているので、このような複雑な形の金属体は、レーダーの方向から見た断面積に近いレーダー断面積を持つと考えればよい。しかし、船体の一部の面がレーダーに正対したときには異常に大きなレーダー断面積となることもあるので、このような複雑な物体は、その反射方向によってレーダー断面積が指向特性を持っている。これに対し、木造船のように電波エネルギーの一部しか反射をしない物体は、その反射波の比率に応じてレーダー断面積が小さくなる。
レーダー断面積をより厳密に定義をすると次のようになる。
『レーダー断面積(Radar Cross Section)とは、ある特定の方向から散乱物体に入射する平面波の単位面積当たりの電力に対する、その特定の方向に散乱する単位立体角当たりの電力の比の4π倍である。更に正確にいうと、散乱物体から散乱電力を測定する点までの距離が無限大に近いときの、その比についてのみこの定義が適用される』(米国電気電子学会IEEE)
この定義を数式で表すと、レーダー断面積σは、その物標(散乱物体)に入力するレーダー電波の電力密度をSo〔W/m2 - 単位面積当たりの電力〕、反射する電力をSr〔w〕とすると、