7・6・7 電圧、電流の有効分の無効分

交流回路において、電圧と電流の間に位相差があるときは、図7・55（a）のよう

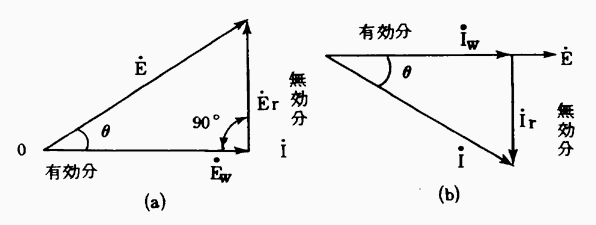
図7・55

に電圧E〔V〕を電流I〔A〕の同相の成分EWとπ/2〔rad〕の位位差をもつErとに分解し、また、図7・55（b）のように電流I〔A〕を電圧E〔V〕の同相の成分IWとπ/2〔rad〕の位相差をもつIrとに分解して考えると便利な場合がある。この関係を式で次のように表す。

EW＝Ecosθ〔V〕、Er＝E sinθ〔V〕…（7・68）

IW＝Icosθ〔A〕、Ir＝Isinθ〔A〕…（7・69）

ここで、EWは電圧有効分、Erは電圧無効分、lW’は電流有効分Irは電流無効分である。これらの式を使って電力と無効電力を示せば次のようになる。

電力：El cosθ＝E（I cosθ）又は＝I（E cosθ）

無効電力＝EI sinθ＝E（I sinθ）又は＝I（Esinθ）

7・7 復習問題（5）

（1）Sin2θ＋cos2θ＝1なることを証明せよ。

（2）sinπ/6、sin π/4、sin π/3、sinπ/2それぞれの値はいくらか。

（3）cosπ/6、cosπ/4、cosπ/3、cosπ/2それぞれの値はいくらか。

（4）電圧の瞬時値e＝Em sinωt、電流の瞬時値i＝Imsin（ωt−90°）の電力P（瞬時値）を計算せよ。

（5）電圧の瞬時値e＝Em sinωt、電流の瞬時値i＝Imsin（ωt−θ）の電力P（瞬時値）を計算せよ。

（6）弧度について説明せよ。

前ページ　　　目次へ　　　次ページ