7・3・2 ベクトル和と合成電流

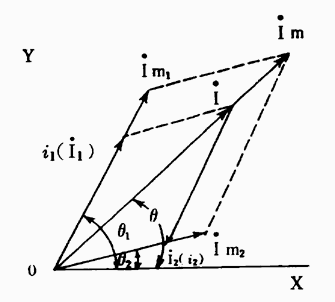
図7・14

図7・14において

i1＝Im1 sin（ωt＋θ1）〔A〕

i2＝Im2 sin（ωt−θ2）〔A〕

のようなi1とi2電流の合成電流をベクトルを使用して求める。

これは、6・2・3によってベクトルの和を求めればよい。即ちIm1とIm2の平行四辺形を作り、その対角線Imが合成電流である。そしてこの場合の偏角はθとなる。この場合には電流の最大値をとったが、実際にはベクトルの長さは実効値を用いることが多い。そしてこの方が便利である。この意味はメータの指示値は実効値であるから、これで画いておけば両者は相似形のため実効値に√2倍すれば最大値のベクトル和が求められる。図中I1、I2及びIは実効値を示し、Im1、Im2及びImは最大値を示している。

7・3・3 正弦波交流の複素数表示

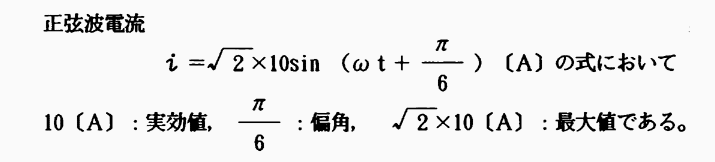
よって上式を複素数で表わす方法を考える。

先づ、このiをベクトルIで表わせば、図7・15のとおりとなる。

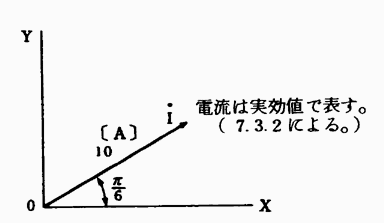
図7・15

次に、これを複素数で表わすには図7・16に示す三角関数を用いることが必要である。

図7・16において、

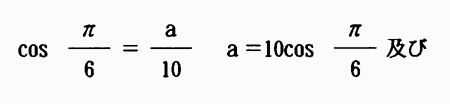
前ページ　　　目次へ　　　次ページ