e3＝Em sim（ωt一β）〔V〕（7・10）

この場合、e2はe1よりも位相（フェイズ）がα〔rad〕だけ進んでいる。また、eはeIよりも位相がβ〔rad〕だけ連れているという。そして、α角及びβ角をt=Oにおけるe2、e3の位相角といい、e1との間の相差角という。また、e1とe2もしくはe3との間には位相差又は相差があるという。

もしも?、及び?コイルが?コイルと同一位置にあれば、位相差はないはずであるから、同じ位相又は同位相にあるという。

7・2・3交流の大きさの表し方

（1）瞬時値と長大値

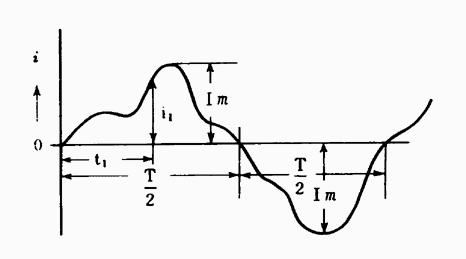
図7・7

（2）平均値1

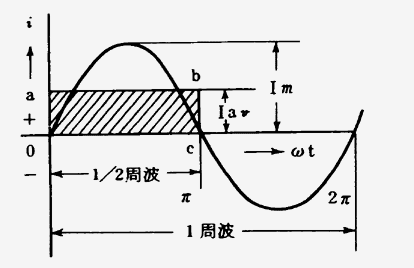
図7・8

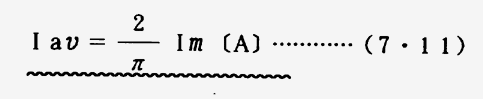
交流の大きさは直流とちがい時々刻々と変わるので直流のように簡単にはいかない。交流の瞬時値及び最大値については7・1でも述べたが、これを定義づければ交流の任意の瞬時の値を瞬時値といい、図7・7ではt1時のiIの値が瞬時値で、T/2のうち最大のImを最大値といい波形の場合には波高値という。例えば、波高率とは最大値と実効値の比をいう。交流の正弦波形では1周波では十側から一側に変化するので、その間の平均を求めれば零の値となる。そこで＋側又は−側の1/2周波の平均値を求める。そこで半波形の面積と等しい面積の長方形oadcの高さを計算によって求めた値をIaνとすれば、次の関係ができる。（図7・8参照のこと。）

前ページ　　　目次へ　　　次ページ