注：上式のSine、cosine、tangentの逆数を次のようにいう。

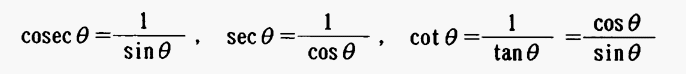
6・1・2直角三角形における三つの角の関係

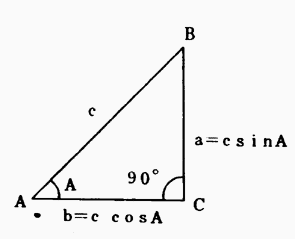
図6・1において、c＝1とすれば

6・1・1における式は次のようになる。

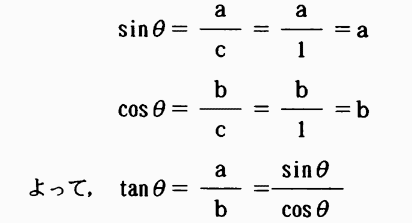
となる。

ここで、このピタゴラスの定理、すなわち、a2＋b2＝12を適用すればsin2θ+cos2θ＝1なる関係式ができる。

注：（Sinθ）2をSin2θで表すが、Sinθ2ではない。Sinθ2とかけばθ2の正弦となるので注意を要する。

また、図6・1の角θ’について考えれば

Sinθ´＝cosθ、cosθ´＝Sinθとかける。

また、三角形の内角の和は常に180°であるからθ´＝90°-θ

それ故にsin（90°-θ）＝cosθ、cos（90°-θ）＝sinθの関係が得られる。

6・1・3直角三角形の解き方

前ページ　　　目次へ　　　次ページ