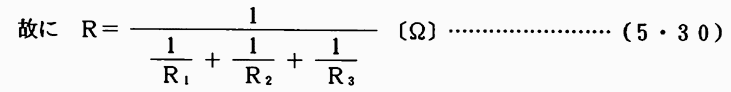
このことはR1、R2、R3、R4……と多数のRn〔Ω〕が並列接続されても、その合成抵抗R〔Ω〕は並列接続の各部の抵抗〔Ω〕の逆数の和の逆級をとればよい。（5・30）式参照のこと。

〔例題〕図5・17においてR1＝10〔Ω〕、R2＝5〔Ω〕、R3＝15〔Ω〕であって、E＝30〔V〕としたとき、この回路の合成抵抗Rは何〔Ω〕か。

また、電流は何〔A〕か。

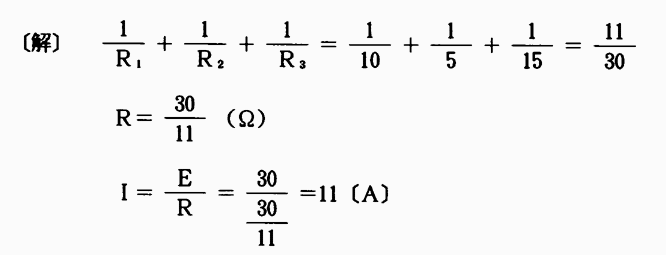
5・9・3直並列接続の合成抵抗

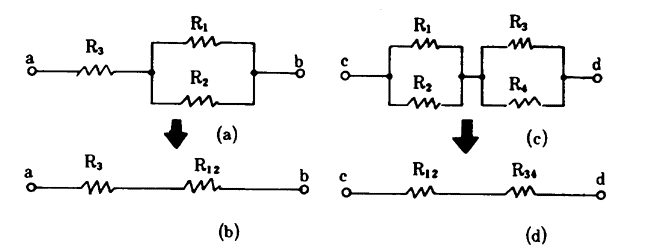
図5・18

図5・18のように、抵抗が直列接続と並列接続が組合わされた場合の合成抵抗の求め方は一般的な公式はない。

そこで、それぞれの回路を単純一な形にして計算するのであるが、最も計算に手間がかからないのは、5・9・1で述べたように直列抵抗に直して合成抵抗を求める方がよい。

図5・18について説明すれば、図5・18（a）では先づR1とR2の並列抵抗を5・9・2により合成抵抗Rl2を求め（同図（b）参照）次ぎにR3+R12の直列抵抗を5・9・1により計算すればよい。また、図5・18（c）の場合はR1、R2及び

前ページ　　　目次へ　　　次ページ