（4）部材の荷重

船底の衝撃圧の分布はWagnerの理論に従うものとして、部材に加わる荷重の評価を行う。先に、水圧センサーによる計測の記述の中で圧力減少係数を紹介したが、パネルや縦骨等の部材にかかる荷重は、衝撃水圧の分布と深い関係を持っている、水面衝撃による水面の盛り上がりが、パネルや縦肋骨に平行な場合、これらに加わる荷重は最も厳しくなる。この時、衝撃圧のピーク部分の拡がりと、パネルの幅の関係でパネルの荷重が決められる。

図−13に示すように、衝撃圧のピーク部のパネルの幅に対する平均を荷重として採用する、これは荷重係数Fgとして、数式で規定されているが、図−14のような傾向を示す。

同様のことが、横桁についてもいえるが、縦部材の場合と若干考え方が異なる。実際には、キールから船側に向かって衝撃荷重が移動する場合を考え、その場合の横桁に生じる曲げモーメント、剪断力を評価して、荷重を設定している。

圧力減少係数についてはAllen＆Jonesの論文5）にも同様の記述がある。Allen＆Jonesは船底スラミング発生時にパネル上で計測された複数の衝撃水圧が、時間、空間的にバラバラであること、これらの平均値が意味を持つらしいことに注目し、高速船に加わる衝撃水圧の数値シミュレーションを実施し、実船計測結果等と合わせて、圧力減少係数という概念をつくった。衝撃水圧のピーク値を推定できれば、対象となる部材の面積と衝撃に関係する全体の面積の比に応じて、圧力減少係数が決まることになる。対象となる部材の面積が相対的に小さいと圧力は高く評価される。この関係式は当初、船種により異なる傾向を持っていたが、最近は統一されているようである。

図−13 船底水圧の分布

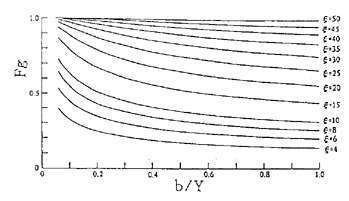
図−14 圧力滅少係数

5. まとめ

水面衝撃水圧について、2次元、3次元の計算法を紹介し、高速船の船底衝撃荷重の推定法への応用について、概要をまとめた、3次元の衝撃荷重計算法はより正確な理論や計算法が発表されており、最近のようにパソコンが高速化、高機能化する時代にあっては、これらを直接、ルール等へ組み込むこともあるかもしれない。少なくとも、設計ツールとして利用できるような方向にはもってゆきたい。

前ページ　　　目次へ　　　次ページ