を表すパラメータとしてばらつきが少ないことによる。

本基準では、正面向かい波での船体運動と波が同調した時の船底衝撃水圧を設計水圧とすることにしているが、波長は比較的に長く、運動は加速度が最大となるような状態を想定している。不規則波中での船底衝撃水圧の5〜10分間の計測値の最大値は、その有義波高と等しい波高の規則波中での同調時の衝撃水圧とほぼ等しいことが実船試験の解析で示されている。

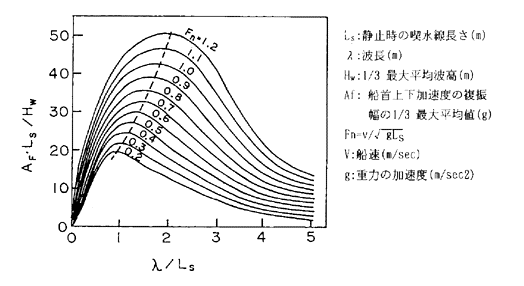
図2.2.1高速船の加速度の応答関数（大隅）

（3）船底衝撃水圧

船底に作用する衝撃水圧はStavovy ＆ Chuangの方法にしたがって、3次元の問題を2次元の水面衝撃の問題に置き換えて取り扱う。Stavovy ＆ Chuangは自らの実験データに基づく実験式により、2次元の水面衝撃水圧（衝撃角が比較的に小さい場合：ピーク値のみ）を与えているが、荷重を考える場合にはピーク値とともに圧力分布が必要であり、力学的にもWagnerの理論式をべ一スにする方がよいことが知られている。（衝撃角が比較的に小さい場合）2次元の水面衝撃水圧はWagnerの理論式、Ferdinandeの理論値がある。

Wagnerの理論では、衝撃角（水面と物体のなす角）が小さい範囲では正しい値を与えるが、衝撃角が大きくなると過大な値を与える。Ferdinandeの理論はほぼ全ての衝撃角に対して成り立つが、部材に作用する荷重の計算等では取り扱いが難しい。両者は小さい衝撃角では一致している。両者とも重力の影響を無視しているが結果は安全側になる。

ここでは取り扱いを簡単にするために、圧力の分布形状はWagnerの理論式と相似になるものと仮定し、水圧のピーク値がFerdinandeの理論値に合うようWagnerの理論式に対して修正係数を設けている。この結果は模型実験結果や重力を考慮した数値解析結果に対しても、実用上問題がないことが確認されている。

（4）衝撃角

衝撃角は水面と物体表面のなす角であるが、3次元の表面形状を有する船体と水面のな

前ページ　　　目次へ　　　次ページ