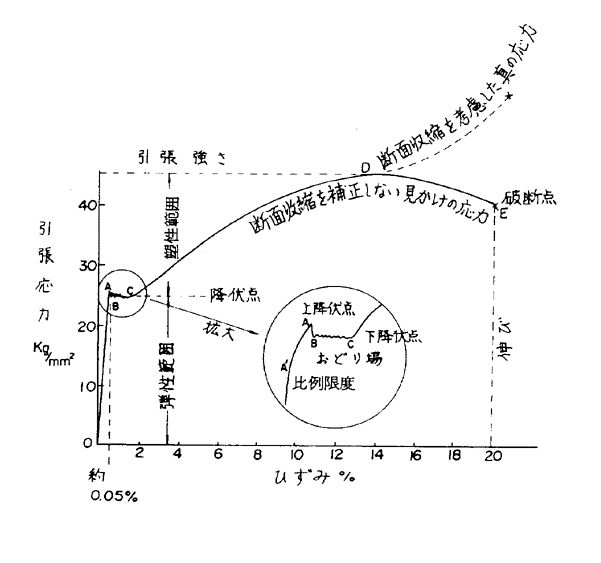
第1.3図　鋼材の応力ひずみ曲線

第1.3図はあとでいろいろと応用するのに便利なように、縦軸に引張応力Ｓ＝Ｐ／Ｗ×Ｔ（?s／?o^２）を、横軸にひずみｅ＝ｘ／Ｌ（単位なし）をとっている。これを応力ひずみ曲線という。

鋼材の応カひずみ曲線の特長について説明しよう。０からはＡ′では非常に急な立ち上がりをもつ直線である。しかしＡ′−Ａではこの直線からややずれている。Ａに達すると応力はＢまでやや下り、Ｂ−Ｃ間では応力はこまかい上下をくりかえして上がらず、ひずみだけが増える。Ｃ点からゆっくりと応力とひずみが増し、Ｄ点で応力の最高値に達し、これから先は断面がくびれ出し、見かけの応力は下がりひずみは増し、遂にＥ点に至って破断する。図に示すように０−Ａ′間を比例範囲、０−Ａ間を弾性範囲、Ｂ点以降を塑性範囲といい、Ａ点を比例限度、Ａ点を上降伏点、Ｂ点を下降伏点、Ｂ−Ｃ間をおどり場と名付ける。Ｄ点の応力を引張り強さ、Ｅ点のひずみを破断時の伸びといい、重要な値である。

比例限度内、すなわち０からＡ′までは応力ひずみ曲線が直線であるが、このことは、応力を２倍とすれば、ひずみも２倍となることを示しており、応力をひずみで割った値をＥで示せば、Ｅ＝Ｓ／ｅが材料によって一定の値をとることとなる。別の言葉で表わせぱ応力とひずみは比例することとなる。そしてこのＥは比例係数の意味があり、これをとくに発見者の名にちなんでヤング係数（または縦弾性係数）とよび、鋼材では21,000?s／?o^２である。

前ページ　　　目次へ　　　次ページ