上の例は１枚の円板を鋼線で固定壁（ここでは天井）に取り付けた場合であったが、次にもっと現実的な例について考える。補・３３図のようにＪ_１，Ｊ_２２個のロータが細い軸でつながれているとする。そして軸受には摩擦がないものとする。この系にはＪ_１とＪ_２とが互いに反対方向にまわり、両者をつなぐ軸がねじれる振動を生じ得る。その固有振動数は

となる。次にもう少し複雑な３個のロータＪ₁，Ｊ_２，Ｊ_３が補・３４図のようにｋ１２とｋ２３のねじり剛さをもつ軸でつながれている場合を考えよう。この場合には振動形態が二通りある。すなわち補・３４図（ｂ）のように系各点のねじれ角の軸方向の分布が直線状になる場合と補・３４図（ｃ）のようにその分布が山形になるものとが出てくる。そしてそれぞれの形の振動が生じる振動数は異なる。すなわち２つの相遠な固有振動状態を持ち、それぞれの振動数に特有の振動形態すなわちモードＭｏｄｅを持つ。固有振動数の値そのものは円振動Ｐについての方程式

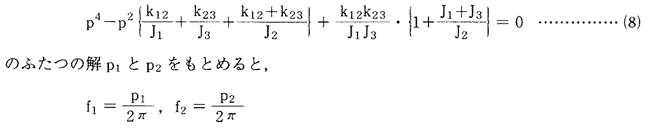
として与えられる。この二つの振動は同時にこの軸系に発生させることができる。したがってそのような場合の各ロータのねじれ具合は一見した場合、補・３４図（ｂ）、補・３４図（ｃ）のようなものではなく見掛け上はかなり複雑なものとなる。さらにこの例から判るようにもしＮ個のロータをそれぞれｋ１２，ｋ２３……ｋN-1Nの剛さを持つＮ−１本の軸でつないだ系ならば１節からＮ−１節までの（Ｎ−１）個の振動モードを持ち、それぞれに対応する振動数をもつ。一般にねじり振動に限らずこのように多くの質量をもち、それに応じた数の固有振動モードを持つ系を多自由度系と呼んでいる。

さて今まで扱った振動系はいくつかの円板と単純な軸というように極めて単純な形で構成されているが、現実にはこのような都合のよい系は存在しない。まず始めの例のばねにはじまってロータをつなぐ軸まですべてそれら弾性要素自身の質量のことは考慮に入れていない。現実には質量のないものは無いから、上記のような議論は限界のあることで、最初の例の場合ならば物体の質量Ｍに比べてばねの質量が十分に小さい、円板やロータの場合もＪ_１，Ｊ_２…に比べて針金あるいは軸自身の慣性モーメントが十分に小さいことが前提になる。しかしそのような前提は常に満足されるというわけにはいかない。例えば実際の軸が補・３５図（ａ）のような太いものであれば軸の慣性モーメントを適当な所に集中させる。例えばこの図に示すように軸上に適当な３点ａ，ｂ，ｃを選び、そこに適当な割合で３分割した軸の慣性モーメントを集中させることにする。そうするとこれはもう５個の慣性モーメントをもつ系であり、４個の固有モードを持つことにする。

　

　

　

前ページ　　　目次へ　　　次ページ