推定式の精度を向上させるために、風圧力係数を流体力の成分で分離する。風圧力は、船体に固定した座標を用い、前後方向風圧力と横方向風圧力の2つの方向成分で表すこととし、回頭及び傾斜モーメントは、横風圧力に風圧力てこを乗ずることにより求める。

　

　小保方ら^7）、梅田ら^8）、烏野ら^{例えば9）}は、水面下船体に作用する流体力の成分分離方法を提案している。ここではこれらの方法を参考にしつつ、Fig. 3で示されるような風による流体力の成分分離を行う。なお、Fig. 3では左右対称な船の相対風向角ψAが0度から90度近くまでの場合を示している。ここでは、相対流速を船体前後方向の主流と、それに直行するクロスフローの2成分に分けて考える。

　

　

　船首から風を受ける場合（図中、a）、船には船体・デッキ上構造物後部での渦放出に伴う粘性圧力抗力及び摩擦抗力が作用する。Fig. 1のX軸方向の力であり、これを主流抗力（LFD）と呼ぶことにする。船首が風向きに対して僅かな迎角を持つ場合（図中、b）は、船体は一種の翼となり迎角に比例した揚力が発生する。この揚力は、小アスペクト比に対する揚力理論で計算が可能な成分であり、翼端から放出される3次元渦によって発生する。その際、同時に自由渦による誘導抗力も発生する。これらをそれぞれ揚力（LI）及び誘導抗力（ID）として分離する。さらに放出渦が翼面に比較的近いところにあることから、非線形の揚力及び抗力が発生し、これらは一般にクロスフロー抗力モデルとして扱われている。これをクロスフロー抗力（CFD）と呼ぶこととする。

　大きな迎角を持つ場合（図中、c）、主要船体の前部背面から自由渦層が流出することになるが、2次元剥離による自由流線の一部と見なし、その影響は、揚力と誘導抗力に含まれているものとする^8）。

　さらに大きな迎角を持つ場合（図中、d）、翼と見立てた船体にはストールが生じることとなる。このとき、揚力と誘導抗力は非常に小さくなり、クロスフローモデルによる粘性圧力抗力が支配的となる。

　次に上記仮定の下、流体力成分の構成、決定方法を具体的に示す。

　主流抗力は、正面風（ψA=0°）と背面風（ψA=180°）の時の風圧力と考えられるから、それぞれの風圧力係数からその係数CLFを求める。このCLFは、相対風向ψAに対して変化すると考えられるので、ψAが0度と180度で1となるようにCOSψAで変化すると仮定する。同様にクロスフロー抗力は、横風時の風圧力係数からその係数CCFを求め、ψAを変数としたCCFsin²ψAで表現する。

　揚力及び誘導抗力の各無次元係数CL、CDについては、小アスペクト比翼に対する揚力理論から次式のように表現する^19）20）。

　

　

　CLIはアスペクト比に依存した係数である。ただし、（5）式は0度から90度の範囲において、ψAの増加に伴い単調増加するため、ストールを含むψAに対する揚力特性を表現できない。そこでFig. 3（d）のようにψAが90度でそれらの成分がOとなるよう、烏野ら^10）と同様に（5）式にCOSψAを乗じることにする。その際、実験結果とそれぞれの成分の特性が一致するように揚力にはCOSψAを乗じ、誘導抗力にはCOS²ψAを乗じた。

　以上の仮定によって、揚力係数C'L及び誘導抗力係数C'Dは次式になる。

　

　

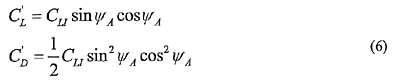
　さらに実験結果によると前後風圧力係数は、ψAが10〜20度と160〜170度付近で増加する傾向ある。理由としてはデッキ上での流れの剥離が前後力に影響しているものと考えられる。この現象を表現するために、sinψAcos³ψAで変化する補正項をさらに足し合わせることにする、横風圧力係数の場合は値が小さく、不明瞭であるため特別な補正を行わない。

　最終的に前後・横風圧力係数は次式のように表される。

　

　

　ここで（7）式右辺第1項は主流抗力、第2項は揚力及び誘導抗力の前後方向成分、第3項は前後抗力の補正項、（8）式右辺第1項はクロスフロー抗力、第2項は揚力及び誘導抗力の横方向成分を示す。（7）、（8）式の各成分をFig. 4に示す。（a）は前後風圧力係数CX、（b）は横風圧力係数CYを示し、「Total」は全風圧力係数値である。「F'XLI & F'ALF」や「F'YLI」は全風圧力係数から主流抗力又はクロスフロー抗力を差し引いた値で、主として揚力、誘導抗力成分と仮定した力である。参考までにF'XLI、F'ALF及びF'YLI成分の関数増減を併せて図示している。

　

　

　各船のCX実験データから、ψAが0度及び180度での値を得て、主流抗力成分F'LFを初めに決定する。また、CY実験データの90度の値からクロスフロー抗力成分F'CFを同様に決定する。残りの成分からCXの場合は最小自乗法によりCXLIとCALFを、CYの場合はψAの10度から30度での平均値を使ってCYLIを求める。このとき、CXとCYの揚力及び誘導抗力係数が必ずしも一致しないことから、CXとCYのそれぞれで求めている。また、船の形状が前後で異なることから、前方、後方からの風による影響を表現するためにψAが0度から90度、90度から180度の範囲で分けて各項の係数を求める。

　（7）、（8）式によって規格化された風圧力係数と元の実験結果との差は、平均でCXの場合7.5%、CYの場合5.3%であった。これらの結果は、全船を対象とし、風圧力係数最大値を基準に全風向角平均で得られた値である。

　

　船体外観形状のみから（7）及び（8）式の各係数を決定する。船体形状の無次元パラメータPiを使って、各係数を次式の線形重回帰式で定義する。

　

　

　ただし、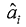はPiの回帰係数である。

　Piの候補としてFig. 2で示された8つのパラメータの組み合わせから次の無次元パラメータを用意する。

（i）長さ関連

　

　

（ii）面積比関連

　

　

（iii）船体形状の特性を表現する面積比

　

　

　著者らが提案した前方法^5）6）で解析時に使用した無次元パラメータを基本的に利用するが、本質的に差異の見られなかった上記パラメータの逆数は今回候補として取り上げない。

　（9）式の構成は回帰分析の一手法である逐次法により決定する^{5）21）22）}。統計的に有意なパラメータを構成要素として順次取り込み、その過程の中で有意でないと判別されたパラメータについては除外する。最終的に式中に含めるべき項が無くなった時点で最終的な解であると判断される。対象とするパラメータが（9）式に取り込まれる際に有意であるかどうかの判定は、次式のF値の大きさによって決定する。

　

　

ここで、

　

　

　ただし、Veは誤差分散、CEjは目的変数の実験値、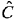jは推定値、nSはサンプル数、nは説明変数の数、Vは分散共分散行列である。

　各項で求まるF値が閾値よりも大きい場合には有意であると判別される（小さい場合はその逆）。有意性を判定する閾値をここでは一般的に使用される2.0とする^21）。さらに項を増加させていく過程において1項のみの単回帰での推定誤差に対して、誤差の減少率が3%未満となる場合をもう一つの目安として計算を打ち切ることにする。このことは、項の増加による解の不安定さを減少させることに寄与する。