|
4. NUMERICAL RESULTS
A ship-ship interaction study was carried out for two ships moving in a channel towards each other (head-on encounter). For each case, the sway forces, and yaw moments were computed as a function of the ships relative distance (measured from bow to bow), and compared with the corresponding experimental results recorded in Dand [9].
In order to facilitate a direct comparison with the experimental data, the governing equations were normalized using the water depth h, a characteristic velocity u = 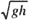 , and a characteristic time T = h/U = 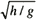 . The Froude numbers are defined by Fnp = U p/U for the passing ship whose speed is U p and Fno = U o/U for the own ship whose speed is U o. Relative Froude numbers are computed as Fnr = Fno-Fnp.
The water-depth-to-draft ratio used was h/To = 1.19, where To = 0.213m is the mean draft of the own ship. The present chimera grid system consists of 7 computational blocks (3 blocks for each ship and one block for the channel) with 811,587 volume grid points and 5 free-surface blocks with 29,895 free surface grid points. A close up bird-eye view of the free surface grid is shown in Fig.4 at two different time instants during the head-on encounter.
The forces and moments are non-dimensionalized according to:
Sway-force coefficient: Cy = Fy/(1/2ρB0T0Up2 (13)
Yaw-moment coefficient: Cn = Mz/(1/2ρB02T0Up2 (14)
where ρ is the water density, Bo is the beam of the reference ship (or own ship). Variables Fy and Mz, are the sway force, and yaw moment experienced on the own ship by its interaction with the passing ship.
Two major studies, a velocity study and a ship-separation distance study, were carried out. The conditions of the cases studied are shown in Tables 1 and 2. Ship separation distance is measured from amidships between the own and passing ships. In both the velocity and the separation distance study, the ships are only allowed to have forward motion. Motions in other degree of freedom are not allowed. This numerical set up is not exactly the same as that in the experiment. However, as can be seen later in the discussion, the sinkage and trim motion do not affect the sway force and yaw moment significantly.
Fig. 4. Own and passing ships for head-on ship encounter.
Table. 1: Velocity Study: h/To = 1.19 Yo/Bo = 1.59
| Case |
Fno |
Fnp |
Fnr |
| 1.1 |
0.128 |
-0.427 |
0.555 |
| 1.2 |
0.172 |
-0.430 |
0.602 |
| 1.3 |
0.250 |
-0.421 |
0.671 |
| 1.4 |
0.329 |
-0.401 |
0.731 |
| 1.5 |
0.369 |
-0.422 |
0.791 |
|
Table. 2: Ship-Separation Study: h/To = 1.19
Fno=0.250 Fnp=-0.421 Fnr=-0.671
| Case |
Yo/Bo |
| 2.1 |
1.10 |
| 2.2 |
1.30 |
| 2.3 |
1.60 |
|
4.1 Velocity Effect
In this study, five cases were explored, as described in Table 1. As in all the cases discussed in this paper, the own ship is at the center of the channel. Figures 5-6 show the sway forces, and the yaw moments obtained for the calculations done for the five cases explored. Each figure also displays the corresponding experimental data. Good agreement can be seen between the calculations and the experimental data. The results seem more accurate for lower velocities. As the velocity increases, higher forces and moments are predicted by the calculation compared to the experimental data.
4.2 Ship-Separation Effects
Three different ship-separation settings were explored for head-on ship motions, as described in Table 2. In all cases, the own ship and passing ship were moving with Froude numbers of 0.250 and -.421 respectively (Fnr = 0.67) . In Figures 7 and 8, the sway forces and the yaw moments for the three cases are plotted. A very good comparison with experimental data can be appreciated. The case with closest ship separation (Yo/Bo = 1.1) seems to be the least accurate when compared to the corresponding experimental data. Since in this case the ships are very close, it would seem that a higher resolution of the girds in between ships would be required to increase accuracy.
4.3 Other Effects
Three additional studies were carried out for Case 2.3 (see Table 2), originally explored in Chen et al. [8].
First, a double-body calculation was done. In Fig. 9, the double-body solution is compared with the original solution, which used a linearized free-surface boundary condition. Two conclusions can be drawn:
1) The magnitudes of the forces and moments of the double-body solution are significantly smaller (〜 3 to 5 times smaller) than their counterparts from the experimental data and numerical results with the presence of the free surface. This is the expected result since there is neither wave resistance nor wave pile up in the double-body solution. This also indicates that the free surface wave generation mechanism is an important portion of the interaction between the two ships.
2) Forces and moments become only noticeable when the ships are passing by in the double-body solution. Since there is no free surface to further carry the wave energy associated with the motion of each ship, the vessels mutual influence becomes noticeable only when they are very close to each other.
A set of unsteady RANS calculations was made for the original ship moving with the sinkage and trim motion recorded in Dand's work. The intent was to understand the importance of the effect of ship dynamics in the interaction of forces and moments. At every time step during the computations, the vertical location of the ship changes and a new grid is generated for the portion of the ship under the mean waterline. The results are shown in Fig.10. These calculations did not show a large difference in comparison to the case without trim and sinkage.
Finally a zero velocity-gradient boundary condition normal to the channel walls (instead of the no-penetration condition) was explored. As can be seen in Fig. 11, t he magnitudes of the interaction force and moment obtained with the zero-gradient boundary condition are similar to those obtained with the no-penetration condition. However, the force and moments obtained with the zero-gradient condition have almost no oscillatory components compared to the one obtained with no-penetration condition (as shown in Fig.3). As a result, filtering is not required for the solution with the zero-gradient solution. Since in the experiment the channel walls may not be perfect wave reflectors, this fact may be better simulated by the second boundary condition. This phenomenon requires further investigation.
|