The ship maneuvering and ship-ship interaction in shallow and restricted waterways are important topics in channel design and ship operation in harbors. The complexity of such problems is related to the shallow-water effects involved as well as the operational conditions of ships moving near obstacles such as banks or other ships. Traditionally, these interactive problems in realistic settings have been approached through experimental means. However, the presence of bank, bottom topography, and other ships require information more sophisticated than the generic modeling of ship-ship interactions used in open water. In this paper, the Chimera RANS method is used to study the ship-ship interaction problem in shallow and restricted waterway. The theoretical formulation, numerical method, and validation of the computation results are presented.

　

 Advanced computational fluid dynamics (CFD) methods are valuable tools to supplement experimental measurements. In the work described in this paper, the particular computational tool of choice was the Reynolds-Averaged Navier-Stokes (RANS) technique. While RANS codes have traditionally been thought of as research tools, recent advances in their efficiency and robustness have catapulted them into the realm of practical design applications.

　

 In this paper, a chimera RANS approach is discussed to study the ship-ship interaction problem in a shallow and restricted waterway. The use of the Chimera RANS method to study this problem has proven a successful approach capable of providing valuable insight. This method can successfully be used to study three-dimensional turbulent flows induced by arbitrary vessel motions in confined shallow-water channels. In the past several years, Chen and Chen [4] and Chen et al. [5] developed a chimera RANS method for the computation of ship-fender coupling during berthing operations. The method was generalized recently by Chen et al. [6-7] for time-domain simulation of large-amplitude ship roll motions including capsizing.

　

 The unsteady RANS equations are formulated in an earth-fixed reference frame and transformed into a general curvilinear, moving coordinate system. In this paper, unsteady RANS computations are done and compared with experimental measurements for ship-ship interaction in shallow water. These comparisons include mostly two ships traveling in opposite directions (head-on encounter) at different speeds and separation distances. The water depth is kept constant in most of the CFD runs. The experimental results were obtained from Dand [9] in the early 1980's. In addition to the passing speed and separation-distance effects, other effects including the importance of the free-surface wave generation by passing ships, ship-motion effects (sinkage and trim), and-tank wall effects are all discussed in the paper.

　

 In order to determine the multiple-ship interactions in a shallow-water navigation channel, the free-surface chimera RANS method of Chen and Chen [4] and

Chen et al. [5,6,7] was used. The method solves the non-dimensional RANS equations for incompressible flow in general curvilinear coordinates (ξ⁽ⁱ⁾, t):

　

　

 where U⁽ⁱ⁾ and u⁽ⁱ⁾ represent the mean and fluctuating velocity components, g^(ij) is the conjugate metric tensor; t is time, and p is pressure. The Reynolds number Re = UL/v is based on a characteristic length L, a reference velocity U, and the kinematic viscosity v. Equations (1) and (2) represent the continuity and mean momentum equations, respectively. The equations are written in tensor notation. Subscripts j and jk, denote covariant derivatives. In the present study, the two-layer turbulence model of Chen and Patel [1] is employed to provide closure for the Reynolds stress tensor .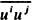

　

 The RANS equations employed in conjunction with a chimera domain decomposition technique have proven accurate and efficient in resolving the turbulent boundary layer and wake flows around the moving and moored ships. The method solves the mean flow and turbulence quantities on embedded, overlapped, or matched multiblock grids, including relative motions. Within each computational block, the finite-analytic method of Chen, Patel, and Ju [2] is employed to solve the RANS equations in a general, curvilinear, body-fitted coordinate system. The overall numerical solution is completed by the hybrid PISO/SIMPLER pressure solver of Chen and Korpus [3] that satisfies the equation of continuity at each time step. The present method was used in conjunction with the PEGSUS program of Suhs and Tramel [10] that provides interpolation information between different grid blocks.

　

 The free-surface boundary conditions for viscous flow consist of one kinematic condition and three dynamic conditions. The kinematic condition ensures that the free-surface fluid particles always stay on the free surface:

　

　

 where η is the wave elevation and (U,V,W) are the mean-velocity components on the free surface. The dynamic conditions represent the continuity of stresses on the free surface. When the surface tension and free-surface turbulence are neglected, the dynamic boundary conditions reduce to zero velocity gradient and constant total pressure on the free surface. A more detailed description of the chimera RANS/free-surface method was given in Chen and Chen [4] and Chen et al. [5,6,7].

　

 In this work, a study of two ships approaching each other moving inside a shallow-water, narrow channel is studied. The validation data used here are the towing tank test results reported by Dand [9]. That experiment study was designed to provide insights into the hydrodynamic interactions between ships moving on parallel courses in shallow water.

　

3.1 Ship Model and Experimental Setup

　

 Two 48.2:1 scaled models were used, 5232 and 5233, whose body plans are shown in Figures 1 and 2. Both models were chosen as representative of "averaged" vessels. Model 5232 represents a single-screw cargo-liner type, while model 5233 represents a tanker. A fully instrumented model 5233 (own ship) was attached to the towing carriage with its track on the tank centerline. Model 5233 has a Lpp of 3.962m, a beam of 0.506m, a draft of 0.208m at EP and 0.218m at AP. Model 5233 was restrained in surge, sway, and yaw, but allowed to pitch and heave freely, and roll to a limited extent. Model 5232 (passing ship) was running on a track and carried no measuring instrumentation. Model 5232 has a Lpp of 3.323m a beam of 0.473m, a draft of 0.162m at FP and 0.170m at AP. Both models were fitted with propeller and rudder.

　

 The model tests were conducted in a towing tank of 90m long, 6.1m wide, and a depth that can be adjusted between 0 and 0.56m. Note that the combined width of the tanker and the cargo liner is about 16% of the tank width. It was decided to model the tank walls in the numerical simulation as solid-wall boundary conditions (no-penetration condition). A zero-gradient wall boundary condition was also implemented for one of the test cases, as discussed latter.

　

 A low-pass filter set at 10 Hertz was used to eliminate the noise originated from the vibration of the towing carriage. In addition, the model test data underwent both a screening process to reject 'wild' data values and a curve-fitting procedure to fit the data into a modified sine function format. The curve fitting strategy was probably influenced by the observations of typical calculations of interactions based on potential flow and rigid free surface flow assumptions. The original measured data was not available in the original report.

　

　

　

3.2 Filtering Technique

　

 In the next section, numerical results for the current study are presented and compared with available experimental measurement in Dand [9]. As discussed before, only post-processed, filtered data is available. In order to have a consistent comparison, the results obtained in the current study were post-processed in a similar fashion as the experimental data were. This post-processing procedure is the subject of this section.

　

 The basic idea with the filtering technique discussed by Dand is fitting a modified sine function that follows the experimental data. This approach can be applied when the data to be fitted follows an oscillatory pattern, which does not diverge. The building blocks are modified sine functions whose dependent variable, τ(t), is given by the implicit function,

　

　

 where Δt is the difference between the t coordinate corresponding to the center of given lobe and the t coordinate corresponding to the peak value of the fitting data for the same lobe. A bar on top of a variable (i.e. 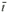or 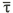) means such variable is locally measured within a given lobe. Within a particular lobe, variable 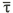is only defined for |Δt| 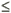T / π , where T is the t length of the lobe. Thus to guarantee that τ always falls within a given lobe, Δt is computed as

　

Δt=Min(T/2-|tp|, T/π) Sign(tc-tp)　(5)

　

 where tc is the center of the lobe (|tc|=T/2), and tp is the t coordinate corresponding to the peak of the input data for the given lobe. This approach is known as time-base distortion (Dand [9]).

　

 The next step is the scaling of the distorted sine curve. In Dand's work, this was done by determining the maximum amplitudes of the fifing data of the considered lobes and next multiplying them by a hyperbolic function of the form

　

seck(αk x)=2/(e^x+e^-x), where x=(t-tp)/T,

　

with αk as fitting parameters. The bell-like shape of the hyperbolic secant function is very reminiscent of the Gaussian function G(x)=(1+x²)^-1, often used in the field of Fuzzy Logic to define membership functions. This shed some insight into Dand's filtering scheme. Though preceding the Fuzzy-Logic boom of the 1990's, that scheme makes use of concepts shared with that discipline. Thus, a Fuzzy-Logic, self-learning system was developed for the filtering scheme, using the same building blocks used by Dand. The filtering function chosen to fit the calculation data was

　

　

 where L is the number of lobes, l is the lobe index,αl are user-given parameters, and Al are the amplitudes associated with each lobe. The parameters αl were chosen as αl=γ/Tl. Thus the selection of the αl's was simplified to the choice of a single parameter γ, whose value ranged between 2 and 3.5. Better results were obtained by computing tp as the weighted average

　

　

 To compute the amplitudes Al, first they are initialized as the maxima of the input data for each lobe. Since the final solution has a contribution of the amplitudes of all lobes [equation (6)], the amplitudes Al must be adjusted to properly representy(t). To this end, first an average ratio between the fitted function yl and the input or reference data Zl is determined for each lobe as

　

　

 where Il is the number of points considered in a given lobe l. The index k represent the cycle number used during the learning process, which is explained below. Using the ratio rl, the amplitudes are adjusted according to:

　

Al(k+1)=Al(k)rl(k)　(9)

　

 Then the condition is imposed that the maxima of each lobe of the yl function never overcome their counterparts from the reference function Zl. To enforce this, an overshoot ratio is computed as

　

Rl(k+1)=Max|yl(ti)[k]/Al(k)|for i=1...Il　(10)

　

 which is used to readjust the amplitudes computed in equation (9) according to,

　

　

 The influence coefficients βlm are computed as

　

　

 The process described by equations (8)-(12) is repeated until convergence is achieved. To improve the solution, a parameter k>1 was used to discard xi rations in equation (8) that exceed kσl, where σl is the mean deviation standard of xi for each lobe l. It was found that as few as 20 cycles are sufficient to achieve convergence in most cases. The process proved to be robust, and no relaxation or learning parameters were required. In Fig.3, two examples are shown with the actual computational results and filtered data for the sway forces and yaw moments on the own ship for Case 2.3 (conditions are specified in Table 2 to be discussed in the next section). The force and moment are plotted as a function of X=Xo/Lo representing the distance of the own and the passing ship in the longitudinal direction; X=0 indicate the bow of the two ships meet each other. In all the comparisons made in the numerical section, filtered data are used.