Abstract: Barge train is one of the main transportation forms in Chinese inland waterways. Its hydrodynamic performance is very complicated due to a variety of combination, water depth, wind and current as well. On the basis of full-scale tests, a kind of Neural Network Recursive Model (NNRM) is established to predict the motion characteristics of a barge train with the environmental disturbances being taken into account. The simulation results have shown that the NNRM can overcome the difficulties brought by the dynamic model.

　

 Yangtze River is the greatest river of China with the length of 6,300 kilometers from west to east. The shipping transportation in it plays a very important role on Chinese economic stage. Barge train is an ideal way of transportation in Yangtze River because of its more capability, lower cost and higher efficiency. However, to precisely predict the maneuvering characteristics of barge train in such inland waterways is wry difficult due to the restriction of waterways and the complicated environmental conditions.

　

 To effectively control ship motion under the complicated environmental conditions is highly desirable to know her maneuvering characteristics, which is commonly expressed by ship maneuvering equations. Nevertheless, the hydrodynamic coefficients in motion equations of the barge train are difficult to acquire since its intrinsical character and the chaotic external effects [1].

　

 In this paper, a neural network intelligent recursive model for predicting the heading, sway, and yaw motion of barge trains is proposed. This Neural Network Recursive Model (NNRM) uses ship motion state variables and rudder deflection as inputs to provide accurate prediction of the vessel's motion. The effectiveness of this method is verified by simulating full-scale tests of a certain barge train in Yangtze River, and the results are satisfactory.

　

 Generally, a barge train consists of several barges and a push boat as shown in Fig.1. Its hydrodynamic characteristic is to a great extent determined by the combination form of the barges. Different combination form gives different characteristic.

　

2.1 The Combination of the Object Barge Train

　

 The following figure shows the object barge train used in the hill-scale tests conducted in Nantong, east China, near Shanghai. The particulars of this barge train are listed as follows:

　

Ship Name: Yangtze 22018

Length: 200m; Breadth: 65m; Mean Drift: 2.6m

　

　

2.2 Brief Introduction of the Full-scale Tests

　

 The full-scale tests are initiated by the engineering project of building a bridge across Yangtze River in Nantong. In order to represent all kinds of ships across the future bridge, the barge train with 16,000 DWTs was chosen and 4 zigzag tests were made, with serial number Test1, Test2, Test3 and Test4. Test1, Test2 and Test4 were conducted upstream, whereas Test3 downstream. The position data was recorded by bow-fixed and stem-fixed DGPS, yaw angle by gyroscope, and time by stopwatch.

　

2.3 Maneuvering Equations of Barge Train

　

 Two right-handed coordinate systems, the space-fixed coordinate system O-X0Y0Z0 and the body-fixed coordinate system G-xyz, are adopted in the description of the maneuvering motion of the barge train, as shown in Fig.2.

　

 X, Y are the components of force vector F acting on the barge train in the body-fixed system and N is the moment about z axis. r is the yaw rate and u, v are the velocity components of the speed V, φ is yaw angle and a is rudder angle.

　

　

 Same as ordinary ships, the maneuvering motion equations for barge train can be written as follows:

　

　

 The terms with subscripts H, P, and R represent the hydrodynamic forces acting on hull, propeller, and rudder, respectively. The terms with subscripts NL and E represent nonlinear and external ones.

　

 The following deduction is based on the assumptions:

　

  1) Both the external and nonlinear terms can be ignored under the condition of mild rudder deflection, say within 15^o.;

　

  2) Force in y direction and moment produced by propeller are negligible since they are small compared to other terms.

　

  3) Force change in x direction is small, that is, the velocity u can be considered constant.

　

2.4 Linearized Maneuvering Equations

　

 For convenience of calculation using the NNRM mentioned above, we firstly linearize the maneuvering equations and then non-dimensionalize all terms. As a result, the following equation is obtained [2]:

　

　

 Here the terms with (') denote non-dimensionalized ones. Eq. (2) is a 1^st order differential equation group, with free terms of rudder force and moment. From the linearized differential equation group, the similarity between v and r is manifest.

　

 Neural Network (NN) has been widely applied to solve ship hydrodynamic problems [3][4][5]. All these efforts are mainly oriented towards sea-going ships or Autonomous Underwater Vehicles (AUVs).

　

 This section is to develop a NN recursive prediction model for simulating the maneuvering motion of barge train s in inland waterways.

　

3.1 Maneuvering Equations in Matrix Form

　

Eq. (2) is easy to be rewritten in the matrix form,

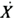= AX + Bu , i.e.:

　

　

 With recalling the full-scale data form, it hints that the application of the proposed method calls for the use of a discrete model in time domain. In the present case:

　

　

 To be consistent with the measured data, the discrete time Δt is given as unitary time. Thus Eq. (3) can be rewritten in discrete matrix form:

　

X(k + 1) = AX(k) + Bδ(k)　(4)

　

 where: x (k), X (k + 1) are discrete state vector on unitary time serial k and k+1; and

　

　

 Eq. (4) gives a recursive way to predict the state vector [v' (k); r' (k)] only if the initial condition is known; and to get the yaw angle φ (k) by integration of r' (k).