|
7・3 正弦波交流のベクトル及び複素数表示
正弦波交流については7・1の図7・3で説明したとおり、Oを中心として腕OAの回転につれてその正射影の変化である、といったがこれをベクトル式に再現すれば次のようになる。
| (拡大画面:8KB) |
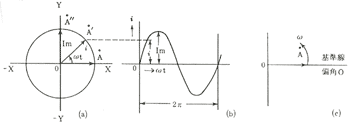 |
図7・12
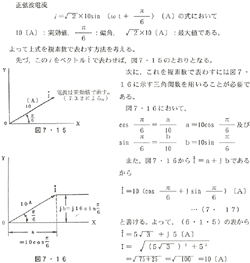
図7・12において電流の瞬時値iの変化は(7・2式)から
i=Im sinωt〔A〕である。
これは  なるベクトルとして考えられる。即ち  なるベクトルはX、−Xの横軸上から出発するから偏角=0である。そして定の角速度ω〔rad/s〕で反時計式に回転し  'ではiの瞬時値は  'の正射影iはY、−Y軸上にあって、  'に至ればI mなる最大値となる。このような正弦波ベクトルとなる。同図(b)は正弦波を示し同図(c)は偏角=0のベクトルを示す。次に、図7・13(a)(b)(c)及び(d)(e)(f)は上記のとおり、同様に考えてよい。
| (拡大画面:17KB) |
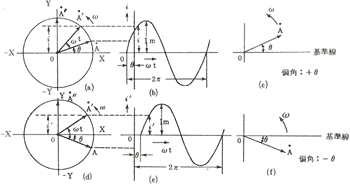 |
図7・13
しかし、前者の図7・13の(a)(b)(c)は偏角θで(+)であり、後者の図7・13(d)(e)(f)は偏角θで(−)である。
これを、それぞれ次のように示す。
i=Im sin(ωt+θ)・・・(7・15)
i'=Im sin(ωt−θ)・・・(7・16)
図7・14
図7・14において
i1=Im1sin(ωt+θ1) 〔A〕
i2=Im2sin(ωt−θ2) 〔A〕
のようなi1とi2電流の合成電流をベクトルを使用して求める。
これは、6・2・3によってベクトルの和を求めればよい。即ち 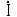 m 1と 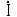 m 2の平行四辺形を作り、 その対角線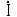 mが合成電流である。 mが合成電流である。そしてこの場合の偏角はθとなる。この場合には電流の最大値をとったが、実際には ベクトルの長さは実効値を用いることが多い。そしてこの方が便利である。この意味はメータの指示値は実効値であるから、これで画いておけば、両者は相似形のため実効値に 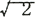 倍すれば最大値のベクトル和が求められる。図中 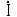 1 1、 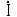 2 2及び 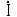 は実効値を示し、 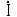 m 1、 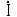 m 2及び 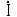 mは最大値を示している。
| (拡大画面:30KB) |
 |
|