|
ARMOR STABILITY OF RUBBLE MOUND FOUNDATION FOR HIGH MOUND COMPOSITE SEAWALL
Masaya Mori1, Yasuji Yamamoto1, Nobutoshi Umezawa1 and Katsutoshi Kimura2
1Civil Engineering Research Institute of Hokkaido
Sapporo, JAPAN
99258@ceri.go.jp
2Muroran Institute of Technology, Muroran, JAPAN
ABSTRACT
High mound composite seawall with slit crown wall is currently under development as a new type of seawall, which is aimed at cost reduction and environmental enhancement. The structure of this seawall allows a high rubble mound, whose mound slope negates the force of most waves by its wave-breaking action. Employment of the slit structure in the superstructure of this seawall enables reduction of wave forces acting on the seawall. The mound slope provides a living environment for seaweed where sunlight abounds.
To clarify the hydraulic characteristics of the high mound composite seawall with slit crown wall, wave forces characteristics and wave-overtopping characteristics have been studied. These studies revealed that the hydraulic characteristics are superior to the conventional seawall. However, sufficient examination has not been conducted on the stability of the armor units of the rubble mound foundation. Therefore, it is not possible to calculate the stable mass of the armor units. We report the results of two-dimensional and three-dimensional hydraulic model experiments on the stability of the armor units for high mound composite seawall with slit crown wall.
INTRODUCTION
At present, the high mound composite seawall with slit crown wall (Fig.1) is being developed as a new type of high mound composite seawall. This structure's rubble mound foundation is high and rubble mound attenuates the energy of breaking waves. The structure's upright section is designed with a slit structure to absorb the wave force and dissipate the overtopping waves. The water above the shallow rubble mound offers an ideal photo environment for seaweed growth.
Several studies have focused on the hydraulic characteristics of the high mound
composite seawall with slit crown wall. Shimosako et al. (1996) reported on their hydraulic model experiment. They clarified the characteristics of wave forces acting on the upright
section. Kimura et al. (1999) and Schuttrumpf
et al. (1999) performed an experiment using a large hydraulic model structure and proposed a calculation
method for wave overtopping rate. They also studied the characteristics of wave run-up height.
However, the method of designing a mound armor unit has not been examined, and some of its aspects remain unknown. Therefore, we made two-dimensional and three-dimensional hydraulic model experiments on the stability of the armor units and foot protection blocks for high mound composite seawall with slit crown wall.
Figure 1. High mound composite seawall with slit crown wall
CALCULATION METHOD OF STABILITY NUMBER
The stable mass of the mound armor units M is usually calculated using the Hudson's formula:
Where H1/3 is the significant wave height, Sr is the specific gravity of the armor units to seawater, γr is the unit mass of concrete, and Ns is the stability number of armor units, which is a function of wave conditions, water depth, structural body shape and armor unit shape.
Tanimoto et al. (1982) reported on their hydraulic
model experiment using irregular waves on the mound armor units of a composite breakwater. They also proposed
a calculation method for the stability number of armor units Ns, using
the dimensionless flow velocity near the mound κ. Fujiike et al. (1999)
examined the stability number of mound armor units on the front wall of breakwater covered with wave-absorbing
blocks. Those researchers introduced a coefficient of breakwater body shape CR
into the calculation method of dimensionless flow velocity κ, to include the effects of the wave-absorbing
effect. Also, they extracted the standard stability number NSO, which
is peculiar for every armor units, from the Tanimoto's formula, to formulate the following equation.
Where h' is the mound depth of the seawall, H1/3 is the significant wave height
Matsuda et al. (2000) reported on the stability
of mound armor units of a high mound composite breakwater. They clarified the relationship between the
impulsive wave pressure coefficient α I proposed by Takahashi
et al. (1992) and the stability number Ns, and calibrated the dimensionless
flow velocity κ. Here, we modify the method of Matsuda et al. (2000) to
calculate the stability number of mound armor units at high mound composite seawall with slit crown wall.
We incorporate the wave-absorbing effects of the slit structure by employing the coefficient of breakwater
body shape CR. In other words, the equation for dimensionless flow velocity
κ is transformed into the following equation, which uses the CR and α I.
| (Enlarge: 12KB) |
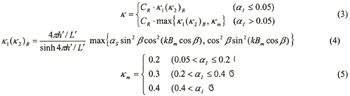 |
Where L' is the wavelength at a mound depth of h', κ is wave number (2π/L'), Bm is berm width, β is wave incident angle, and αS is correction coefficient, αI is the impulsive wave pressure coefficient.
EXPERIMENTAL METHOD
2-D test
The two-dimensional wave flume was used in the cross-sectional experiment. The flume length, height, and width were 28.0 m, 1.0 m, and 0.8 m, respectively. The model structure (Fig.2) was placed horizontally and connected to a sea bottom slope whose gradient 1: 30. The model structure was set at the water depth h of 26.0 cm. The water depth of mound crown h' was varied 0cm, 4.0 cm, and 8.0 cm. Two types of upright section were used: a wave-absorbing section with slit crown wall and a vertical section with conventional upright wall. This allowed comparison of the armor unit stability between different structures. The width of wave chamber for the wave-absorbing section was 22.0 cm, and the opening ratio of the cylindrical slit section was 15% based on a frontal view. The experimental waves were all irregular. The wave height H1/3 ranged from 5.0 to 15.0 cm. The period T1/3 was 1.4s, 2.0s, and 2.6s. The cross-sectional experiment was performed for two wave conditions. In one condition, 3,000 waves were continuously generated and progress of damage was measured. In the other condition, 500 waves were generated in separate groups, and the wave height was raised gradually to enable calculation of the stability limit wave height. During the experiment, armor units were not fixed, even if the damage was generated. The experiment employed flat armor units weighing 66 g, 100 g, and 140 g. The stability number NS was calculated for the damage level of 1%. Damage was defined as movement by more than half the length of the armor unit.
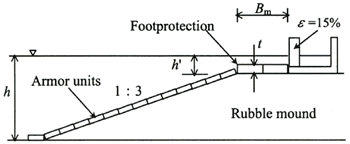 Figure 2. Cross section
3-D test
A three-dimensional experiment was made with a wave basin of length 23.3 m, width 28.2 m, and depth 1.0 meter. A 6.8-m-wide detached structure was installed. The incident angle was set at 0° and 45 degrees. The relative mound depth h'/h was 0.2. The other conditions were the same as those of the two-dimensional experiments. The experiment employed foot protection blocks, whose length and width were set constant at 10.0 cm and 5.0 cm, respectively, and whose thickness t was alternated between 1.0 cm and 2.4 cm. Horizontal movements of 10.0 mm by the foot protection blocks were set as the critical value of stability.
Figure 3 shows the relationship between the number of waves N and the damage level of armor units D. Here, the wave height and the period were set at 11.2 cm and 1.4s, respectively, and there were three relative mound depth h'/h. For each of the three ratios, the damage does not progress after the application of the first 500 waves. The damage ratio is greatest when h'/h is 0.15. Even when the mound depth decreases, the damage does not necessarily increase. Photo 1 depicts the damage after 3,000 waves. The photo at left shows the damage when h'/h = 0. The photo at right shows the damage when h'/h = 0.15. At these two ratios, armor unit displacement occurred at almost the same location on the mound slope.
Figure 3. Progress of damage
Photo 1. Damage location
|