|
PREDICTION METHODS FOR A HYDROELASTIC BEHAVIOR OF AN AIRCUSHION SUPPORTED ELASTIC FLOATING STRUCTURE
Tomoki Ikoma1, Koichi Masuda1, Hisaaki Maeda1 and Chang-Kyu Rheem2
1Department of Oceanic Architecture and Engineering, College of Science and Technology
Nihon University
Funabashi, Chiba, JAPAN
ikoma@ocean.cst,nihon-u.ac.jp
2lnstitute of Industrial Science, University of Tokyo
Meguro-ku, Tokyo, JAPAN
ABSTRACT
This paper shows the two prediction methods for the analysis of hydrodynamic forces on an aircushion-supported elastic floating structure. One is an approximate method in which the zero draft is assumed and the pressure distribution method is applied, therefore, the problem becomes two-dimensional horizontally. Another applies the three-dimensional source distribution method. There are some areas of free water surface in the aircushions. A behavior of the free surface in the aircushion is directly considered in the analysis of the water pressures or the velocity potentials. In the results the validity of the zero draft assumption is proved. Additionally, a characteristic of the elastic deformation is discussed in head sea conditions. It is found that the elastic deformation is little and the heave motion mode becomes very small when a whole bottom of the floating structure is the aircushion. However, when structural surfaces at the bottom are wide, i.e. not air-supported areas are large, there are some cases that the deformation increases because of the resonance phenomenon. We will investigate the water wave behavior around the floating structure, and from the wave behaviors we will examine the wave drifting forces.
INTRODUCTION
There are some methods for the hydroelastic response reduction on pontoon-type flexible floating structures. One method is the added mass increases due to installation of submerged horizontal plates at part of edge of the structure. Another is a method such as phase of an elastic wave of the flexible structure being shifted to devise a shape of an area of end of the structure. However, the wave drifting force may increase due to reducing the elastic deflection while the above methods can reduce the elastic deflection. Increase of the wave drifting force is possibly a problem for a design of a mooring system.
As a countermeasure, the authors have proposed a very large floating structure with wave energy absorption devices applying the oscillating water column. Its concept was that the device absorbing the wave energy prevented an increase of a reflection wave due to the reduction of the deflection. However, it was very difficult to optimize the device. In addition, the wave drifting force was not always reduced efficiently because the transmitted wave did not change although the reflected wave decreased. Originally, it was the best method for a reduction of the wave drifting force that the reflection wave makes to decrease and the transmitted wave makes to increase but a pontoon-type flexible structure cannot satisfy the above things simultaneously. However, if only water waves can be transmitted no matter if the structure doesn't deform elastically, the transmitted wave will not decrease. Therefore, it may be possible to reduce the wave drifting force. A type that the above problem may be settled is an aircushion supported floating structure.
The analysis method of hydrodynamic forces and characteristics of a rigid motion
of an aircushion supported floating structure were investigated by Pinkster
et al. (1998, 2001) and Lee et al. (2000). These investigations were carried
out with a three-dimensional problem for the analysis of hydrodynamic forces, however only rigid motion
modes were considered in the investigations. Therefore, characteristics of hydroelastic responses of a
very large flexible floating structure supported by aircushions have not been concretely discussed.
The present paper shows qualitative characteristics of a hydroelastic deflection
of aircushion supporting very large floating structures, and an effectiveness of such floating type is
verified. The analysis method and formulations are shown. The pressure distribution method, by Maeda et
al. ( 1996, 2001), is applied. The zero draft
is assumed in this method. The pressure change in an aircushion is linearized and a boundary condition
of a free surface in an aircushion is directly considered in the analysis of pressures ( Ikoma
et al., 2002). In this paper, basic characteristics of the elastic deflections of the large aircushion
supported elastic floating structures are examined. We examine the hydroelastic behavior of the structures
in not only head sea conditions but also oblique sea conditions. We confirm the effectiveness and discuss
the behavior of the waves around the floating structure.
THEORY
Equation of pressure in aircushion
Originally, the boundary condition of the general free surface is given as the equilibrium of the pressure between the pressure of the free surface and the atmosphere. In case of the boundary condition on the free surface in the aircushion, the pressure on the free surface is balanced with the compression pressure in the aircushion so far. If the adiabatic compression is assumed to the pressure change in the aircushion, the equation of the pressure can be expressed such as:
| (Enlarge: 3KB) |
 |
where, P 00 stands for the atmospheric pressure, P m
stands for the additional hydrostatic pressure due to sinking by its weight, V 0
is the initial volume of the aircushion; γis the specific heat ratio (1.4 is used in this study) and 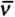 stands
for the volume varying value of the aircushion. After here, the initial pressure in the aircushion P 0
is expressed as follows:
The pressure in the aircushion varies non-linearly according to the volume change. Since the hydrodynamic force is analyzed by using the linear theory. it is necessary that the relation between the pressure and the volume change be linearized. If the relation between the volume change and the initial volume of the aircushion could be expressed as follows:
The following approximation was possible:
Therefore, equation (1) can be rewritten as follows:
The volume of the aircushion changes according as the water level varies and a ceiling of the aircushion deforms elastically.
Three-dimensional prediction method
The three-dimensional singular point distribution method (3D-SDM) ( Maeda
et al., 2001) is applied to the analysis of the velocity potentials. In this study, this method is
applied to the analysis of a VLFS with the aircushion with the definitions of boundaries shown in Figure
1 using the right hand Cartesian coordinate. The vertical axis z is the positive upward. A region of water
mass under the aircushion and surrounded by a skirt is defined as an inner region Ω A.
Outside region of the water mass is defined as the outer region Ω. The area between the inner region and
the outer region is continued by a matching boundary. The former includes a free surface in the air chamber.
The matching boundary at the bottom outlet satisfies the continuity condition of the velocity potential
and the velocity flow. The multi domain method is applied to the 3D-SDM. The free surface in the aircushion
satisfies the equation (5).
Figure 1. Definitions of boundaries
The Laplace's equation is satisfied in the fluid region:
∇2φ=0 (6)
Each boundary condition is listed as follows;
| (Enlarge: 24KB) |
 |
Where, subscripts z and R represent the differential due to z
or R. And, K is ω2/ g , k is a wave number,
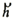 is a normal vector and 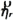
stands for a mode shape function of the γ-th motion mode. Subscripts D and I mean
the component of the diffraction or incident wave. P0 is an initial pressure
in the air chamber, V0 is an initial volume of the air chamber,ρis fluid
density, g is the acceleration of gravity, ωis angular frequency, Δz represents vertical
displacement of the water surface in the air chamber and i means a complex number. γstands for
the specific heat ratio, and γis 1.4 in this study.αrepresents the complex coefficient, which expresses
the phase of the pressure corresponding to the volume change in the air chamber. Therefore, amplitude
of α is defined from 0.0 to 1.0. It is possible that this is expressed as the impedance of the orifice.
In addition, subscripts O and A in equations (12) to (16) stand for the outer region and
the inner region respectively. In the diffraction problem, there is no component of the velocity potential
of the incoming wave.
The source density can be obtained solving the integral equation based on the above boundary conditions, and the velocity potentials are obtained later. The integral equation in the air chamber is expressed as:
For Diffraction problem:
| (Enlarge: 5KB) |
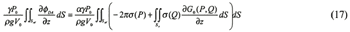 |
For Radiation problem of r-th motion modes:
| (Enlarge: 6KB) |
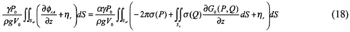 |
Where σ represents the source density, and the Green function in the infinite fluid G0 is 1/r(P,Q), which is a fundamental solution of three-dimensional Laplace's equation.
|