|
2.3.2 数値計算による離岸流の再現および検討
(1)数値計算の目的
4年間にわたる現地実測の結果、離岸流に海底地形が与える影響は非常に大きいことが分かった。しかし、同じ地形上でも入射波特性などの変化によって離岸流の特性が変化することを前年度調査結果として報告した。ここでは現地観測で測量された地形上での計算により数値計算の精度を検証し、さらに潮位や波向きも含めた波の場の変化によって地形性離岸流がどのような挙動を示すのかを調査することを目的とする。
(2)計算手法および基礎式
計算には、まず計算地形上での波の変形を非定常緩勾配方程式を用いて計算し、求められた波高分布を用いて海浜流基礎式を解くことで流れの場を計算する。
非定常緩勾配方程式として西村ら(1983)の式を用いる。西村らははじめに線流量から方程式に相当する式を導き、これを緩勾配方程式に代入することにより連続式に相当する式を導いた。基礎式は以下のようになる。
ここで
η:海底勾配の0次のオーダーを満たす線流量ベクトル
Q':水面変動量
c:波速ベクトル
n:浅水度係数
また海浜流基礎式はNavier-Stokes方程式および流体運動の連続式を鉛直方向に積分にし、時間平均をとることによって求められる。座標系を汀線直角沖方向にx軸を、静水面沿岸方向にy軸を、鉛直海底方向にz軸をとると基礎式は以下のように表される。
ここに、U, Vは断面平均された岸沖および沿岸方向の時間平均流速、 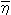 は平均水位変動量、hは水深、τ x, τ yは岸沖および沿岸方向の底部せん断力、S xx, S xy, S yx, S yyはradiation stressである。 Radiation stressは以下式で与えられる。
水平混合係数はLonguet-Higginsらに倣い次式を用いる。
ここでNは無次元定数である。
底部せん断力τx, τyは椹木らによって提案されている次式を用いる。
ここに、Uwは波による底部水粒子速度振幅、fwは摩擦係数であり、Stewartによる次式を用いる。
式中のamは水底での水粒子軌道の最大振幅、ksは粗度高さである。
計算においては式(2.3.3)、(2.3.4)、(2.3.5)をADI法を用いて計算した。これは計算のタイムステップを2分し、前半のΔt/2では式(2.3.3)、(2.3.4)をz軸方向の成分にはimplicit表示、y軸方向にはexplicit表示をし、連立してU、 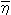 を求める。後半では式(2.3.3)、(2.3.5)をz軸方向にexplicit表示、y軸方向にimplicit表示してV、 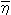 を求める。この方法の利点として、 (1)X、y方向の変数がそれぞれ交互に一方向のみimplicitな差分で表現するため、計算式が簡単になる。
(2)X、y方向でimplicitとexplicitの差分表現を交互に繰り返し計算をするので、誤差の増大が相殺されるため計算の安定性に長ける。
という点がある。
|