|
1・5・7 共振条件
直列共振
並列共振
(1)条件 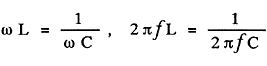 (2) 共振周波数 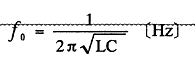 〔例題〕インダクタンスLが0.1〔H〕のコイルに、容量Cが0.1〔μF〕のコンデンサを直列に接続した回路の共振周波数 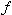 0 0は何〔Hz〕か。 〔解〕
上図のようなホイートストンブリッジ回路においてX抵抗を求めようとするにはSを適当に調節して検流計Gの指針が零にまで調節したときに、次の平衡条件で求められる。
S.P.及びQの値は既知のものとする。
〔例題〕ホイートストンブリッジを用いて未知抵抗Xを測定しようとしてP=10〔Ω〕、Q=100〔Ω〕とし、Sを調整して151〔Ω〕としたら、検流計Gの指針は零をさした。
Xの値は何〔Ω〕か。
〔解〕 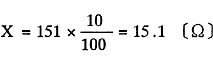
(1)△結線
(2)Y結線
(3)相電流
(4)平衡三相負荷電力
(注):(1)Pは英語の相phaseの略、 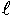 は英語の線間lineの略 (2)各相線間電圧と線電流との間の位相差は(30°+θ)〔rad〕である。
〔例題〕1. Y−Y回路で、相電圧の大きさが100〔V〕で、負荷の一相が20〔Ω〕の抵抗がある場合の、相電流Ip1、Ip2、Ip3はどのように表されるか。
〔解〕
〔例題〕2. △−△回路で、電源の相電圧がそれぞれ200〔V〕、負荷の各相のインピーダンスZが20〔Ω〕で、負荷に流れる電流は、電源の相電圧より30°遅れている。この回路の線電流の大きさ 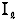 及び線間電圧と線電流の位相差θ〔rad〕はそれぞれいくらか。 〔解〕
線電流は相電流より30°遅れているから、位相差θは、θ=30°+30°=60°遅れている。
〔例題〕3.
上図の三角結線の負荷に加えた線間電圧 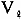 は200〔V〕で、各相のインピーダンスZはそれぞれ等しく、R=3〔Ω〕、X L=4〔Ω〕であるときの線電流〔A〕、負荷の偏角θ〔rad〕、力率〔%〕及び電力〔kW〕を求めよ。 〔解〕 インピーダンスZ〔Ω〕は1・5・5により次の関係式から求めることができる。
n個のコイルを2π/n間隔で配置し、これに対称n相交流を通ずると電流と同じ周波数の一定速度で回転する不変回転磁界ができる。(三相誘導電動機の固定巻線には回転磁界ができることはその例である)
合成回転磁界の大きさ 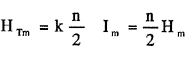 Im:各相電流最大値、Hm:各相で作る磁界の最大値
k:係数、n:相数
単相、二相、三相などの例
| (拡大画面:20KB) |
 |
| (注): |
三相の場合は回転磁界ができるため始動回転力があるが、単相の場合は交番磁界のためこのままでは始動回転力(始動トルク)がない。 |
(1)回転磁界の回転方向
位相の遅れている相の磁界のほうへ回転する上図において時計式方向となる。
(2)逆転
三相のうち二つの相を入れ替えると、回転磁界は上図において反時計式の方向に回転する。
|