Fig.15 |
CL-CD curve on the various sails [SRS;Square Rigid Sail,SSS;Square Soft Sail, RWS; Rigid Wing Sail, TSS; Triangular Soft Sail] |
Fig.16 |
Polar curve of CX on the various sails [SRS;Square Rigid Sail,SSS; Square Soft Sail, RWS; Rigid Wing Sail, TSS; Triangular Soft Sail] |
Essentially, it is thought that the sail form influences on the induced drag broken out on the soft sail, but it is clarified that the influence of that is very small in the experiments.
2.4.2 CLMAX and Maximum CL/CD
Fig. 12 shows the maximum lift coefficients CLMAX as open marks and the values of the maximum CL/CD as closed marks obtained from Fig.9〜Fig.11. In case of an ordinary wing, the lift-curve slope and CD/CL2 are usually used as the index of the performance of the wing. Here, the maximum CL/CD that influences on the performance of sailing on the wind is shown in the figure. The horizontal axis of the figure shows the aspect ratio AR.
|
Fig.17
|
Grid example of the calculation on the hybrid-sail(LH2, β=35deg, γ=20deg)
|
|
Fig.18
|
Aerodynamic characteristics of the hybrid-sails comparing the calculation results with the experimental ones
(LH2, β=35deg, γ=20deg)
|
Practically CLMAX and the maximum CL/CD increase as the AR increases. This is the same tendency that the conventional wings of higher aspect ratio are observed to have higher lift-curve slope [6].
2.4.3 Effect of the slat, the rigid wing sail and the soft sail
The effect of the each element on CLMAX is investigated using the LH6 model. The CLMAX of PH1 and PH2 are same level. That of PH3 is very small compared with the others. This figure shows the lift of the hybrid-sail is mainly caused by the slat and the soft sail, and the influence of the slat is very large though the lateral project area of the slat is about half of that of the soft sail.
2.4.4 Size effect of the slat
It was clarified that the influence of the slat is very large from Fig.13. It is preferable, however, that the slat size is as small as possible when the sail is equipped with the slat actually from the structural viewpoint. Hence, the influence of the slat size was investigated. Fig.14 shows the result of CLMAX and CD at CLMAX in case of the sails with the large slat and the small one. As shown in Table 1, LH1 equips with the large slat that has 0.1m chord and 0.1m circular arc. SH1 equips with the small slat that has 0.05m chord and 0.1m circular arc. Each different lateral projected area S is used in Eq.1. As a result, there is no large difference on CLMAX between LH6 and SH1. Although CLMAX of Sh1 may decrease and the difference may become large in case of the same AR as shown in Fig.12, it is clear that even the small slat is efficient.
2.4.5 Comparison of the experimental results on the various sails
Fig.15 shows the comparison between the results of the present experiments and those of the previous sails already presented [7]. No.1 in the figure is the square rigid sail. No.2 is the square soft sail and No.3 is the rigid wing sail with a triangular soft sail. The AR of three kinds of the sails is about 2. The lift coefficient of No.5(LH1) presented in this paper is much larger than that of No.1〜4.
Fig.16 shows CX value at the polar graph on the sails shown in Fig.15. Maximum thrust coefficient of No.5(LH1) is about 2.7 in 110deg wind direction. The important point to gain the large thrust when 90deg<θ<180deg is that the lift is not only large, but the drag is also large as in the equation(2). However, even if the aspect ratio was changed in this experiment results, a big difference was not seen in the drag coefficient either in Fig.9. Therefore, it is necessary to increase the lift coefficient by enlarging the aspect ratio as much as possible to gain the much thrust. The hybrid-sail presented in this paper is shown to have high performance on the thrust, but the mechanism of the sail is a little complex compared with the previous square sails.
3. CFD CALCULATIONS
When a new type sail is examined like this time,there are many combinations of parts and positions in order to seek the best performance of the sail, and it is difficult to cover all characteristics of them by the model experiments. It is in the current state that examinations of the aerodynamic characteristics can be carried out comparatively easily by CFD calculation. Therefore, the lift and the drag of the square hybrid-sail used in the experiments were calculated to confirm efficiency of CFD in deciding the specification of the sail, and the results were compared with those of the experiments.
3.1 Numerical method
The calculations were carried out using packaged software 'Storm/CFD2000' supplied by Adaptive Research [8]. 'Storm' is general-purpose computer program designed to numerically solve the Navier-Stokes equations, which consist of conservation equations for mass, momentum and energy.
3.2 Governing equations
The conservation of mass and Newton's second law applied to the fluid passing through a small fixed fluid volume are expressed as follows:
Where ρ;fluid density, t;time, x i;position vector in the i th coordinate direction, u i;i th-fluid velocity component, B i; component of the total body force per unit volume, ρ; local pressure, and 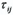 is the viscous stress tensor given by
Here, μ; dynamic viscosity of the fluid due to laminar diffusion, δij;the Kronecker delta function.
3.3 Algorithm
The code uses a finite-volume representation of the governing equations. 'Storm' uses the PISO (Pressure Implicit with Splitting of Operators) algorithm developed by Issa [9] and Issa et al. [10] to solve the coupled system of governing equations. The solution algorithms chosen for the flow solver were incomplete LU decomposition for pressure and the Alternating Direction Implicit (ADI) method for all flow velocities. The convective terms in the governing equations were modeled using second-order up-wind scheme which discrete using central differencing. The diffusive terms were modeled using an arithmetic mean interpolation scheme for evaluation of the transport coefficients between cell faces.
|
Fig.19
|
Comparison between the calculation results and the experimental ones on relative CL in case of the different boom angle(LH2, α=20deg, γ=30deg)
|
|
Fig.20
|
Comparison between the calculation results and the experimental ones on relative CL in case of the different slat angle
(LH2, α=20deg, γ=30deg)
|
3.4 Model description
The LH2 sail was used in the calcuation. As for example, the model geometry and the mesh are shown in Fig.17. From the Specification of the target hybrid-sail, 2-D calcuation was done using BFC grid in this paper. The coordinate and the definitions are defined as same as the previous section. The soft sail has average curvature in the vertical obtained from the three-dimensional measurement using stereovision. The flow domain of the model is 3.5C long in the X-direction, 2.3C long in the Y-direction as the representative length C that is the total sail chord. The flow domain was divided into six sections in the X-direction and five sections in the Y-direction. The mesh was stretched towards the sail to increase cell density near the sail and it contains 170 cells in the X-direction, 120 cells in the Y-direction for a total of 20400 cells.
3.5 Boundary and calculation conditions
The flow was computed by the laminar solution. No slip condition is given on the sail surface. The density was based on the ideal gas. The Reynolds number is 2.2×l05 in the 8.0 m/s wind velocity as same as the experimental condition. The constant for 1.0×10-4 seconds at time interval was used and the duration time is 1.5〜2 seconds in the calculation when the steady solution has been obtained.
3.6 Calculated results
The calculated results were compared with the experimental ones as shown in Fig.18. The open diamonds stand for the experimental and the closed squares for calculated results in the figure. The calculated results are in the overestimation because of not including the 3-dimensional effect of the sail, but the tendency between experimental results and calculated ones agrees with each other.
The influence of the boom angle and the slat angle was investigated in the calculations. We have already gotten the results that the influence of the bend of the sail is very small. Hence, in these cases, the calculations were done by the condition that the sail is flat. The results were compared with the experimental ones in Fig.19 and Fig.20 by a relative evaluation. The maximum values are obtained at γ=30deg in Fig,19 and at β=35deg in Fig.20. As a result, CFD is very useful to investigate the performance of these kinds of sails because the experimental results and calculated results have same tendency on the maximum lift coefficient.
4. CONCLUSIONS
As the reference of the future work to build the oceangoing sailing ship, the aerodynamic characteristics of the hybrid-sails were investigated experimentally and computationally. The results may be summarized as follows:
(1)The effectiveness of the present hybrid-sails consisting of the rigid wing sail, which plays the role of a mast, the slat and the square soft sail was confirmed by comparing with the previous sails.
(2) The lift coefficient almost increases as the aspect ratio increases in the experiments. On the other hand, the drag coefficient does not change largely in that case.
(3) The influence of the slat and the soft sail on aerodynamic characteristics was investigated in the experiments. It was understood that the influence of the slat on the lift is very large.
(4) The maximum lift coefficient was obtained as 2.6 and the maximum thrust coefficient as 2.7 by the optimum setting of the hybrid-sail.
(5) It was shown that CFD is very useful to investigate the performance of the hybrid-sail by relative evaluation even if the sail has complex shape like this time.
ACKNOWLEDGEMENTS
The authors are greatly indebted to Dr. Kunihiro Hoshino in our research institute for measuring the sail surface curvature in the wind by the three-dimensional measurement using stereovision.
REFERENCES
[1] Matsumoto N., Inoue M, and Sudo M, "Operating Performance of a Sail Equipped Tanker in Wave and Wind", Second International Conference of Stability of Ships and Ocean Vehicles (STAB), pp451-464, 1982
[2] Usuki lron Works Ltd "International Voyage Sail-equipped Bulk Carrier 'USUKI PIONEER' ", Funenokagaku, Vol.38, pp36-43, 1985 (in Japanese)
[3] Fujiwara T., Hirata K., Ueno M. and Nimura T. "On Aerodynamic Characteristics of a Hybrid-Sail with Square Soft Sail" The Proceedings of the Thirteenth International Offshore and Polar Engineering Conference (ISOPE2003), Hawaii, USA, 2003
[4] Nojiri T., Sano K., Yagi H., Inoue H. "Hybrid Sail developed to show Max. Lift coefficient of 2.42 for Large Vessels -Reduction of Fuel Consumption and C02 Gas Emissions Expected-", MITSUI ZOSEN TECHNICAL REVIEW, No,178, pp.132-138, 2003
[5] Minami Y., Nimura T., Fujiwara T. and Ueno M. "Investigation into Underwater Fin Arrangement Effect on Steady Sailing Characteristics of a Sail Assisted Ship", The Proceedings of the Thirteenth International Offshore and Polar Engineering Conference(ISOPE2003) , Hawaii, USA, 2003
[6] Abbott I.H. and Doenhoff A.E.V. "Theory of Wing Sections", Dover Publications Inc., 1959
[7] Ishihara M., Watababe T. et al "Prospect of Sail-Equipped Motor ship as Assessed from Experimental Ship 'Daioh' ", Shipboard Energy Conservation Symposium, The Society of Naval Architects and Marine Engineers, ppl81-198, 1980
[9] Issa R.I. "Solution of the Implicitly Discretized Fluid Flow Equations by Operator-Splitting", Journal of Computational Physics, Vol.62, pp40-65, 1985
[10] Issa R.I., Ahmadi-Befrui B., Beshay K.R. and Gosman A.D. "Solution of the Implicitly Discretized Reaching Flow Equations by Operator-Splitting", Journal of Computational Physics, Vol.93, pp388-410, 1991.
AUTHOR'S BIOGRAPHY
Toshifumi Fujiwara is the Chief Researcher, Manoeuvring and Control Group, Department of Maritime Safety, National Maritime Research Institute (NMRI), Japan.
1994: Researcher, Planning Department, Ship Research Institute (SRI), Ministry of Transport, Japan
1995: Researcher, Ship Dynamics Division, SRI
1998: Chief, Safety Standards Division, Maritime Technology and Safety Bureau, Ministry of Transport, Japan
2000: Researcher, Ship Dynamics Division, SRI
2002: the present post
|