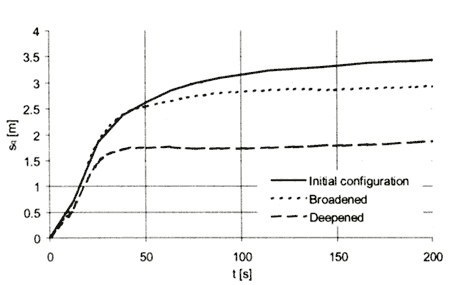
For the maintenance of the fairway it may be good to know whether it would be better for the ship's behavior to deepen or broaden the fairway. Fig. 7 compares the time-varying squat computed by the program BEShiWa for the PANMAX containership moving at a speed 17.68 knots on a near-shore fairway. The initial configuration (solid line) has a section of 100m width and 15m deep. The deepened case (dashed line) has a depth of 19 m and the broadened one (dotted line) has a width of 144m. By a deepening of 4m, ca. 25% of the initial depth,the asymptotic squat has been reduced to 50% of the value at the initial configuration. By a broadening of 44 m, implying the same sectional area as the deepened case, the squat has been reduced only by ca. 15% of the value at the initial configuration. As expected, the deepening is an obvious measure for reducing the ship's squat.

　

　

　

 As discussed by Fluegge and Uliczka (2001), model tests shown there are strong interaction of the ship's squat with the bottom topography. For a special configuration of the floor characteristics, i.e. the length of a periodically trackwise changed bottom, with the ship's length and speed, a resonance of the vertical motions of the ship could be excited. Such a resonance would be very dangerous and should be avoided. In principle, the present numerical method can be used to examine such unsteady cases. Fig. 8 shows the space-varying squat computed by the program BEShiWa for the PANMAX containership moving at a speed 18.86 knots. The three artificial, laterally unbounded bottom topographies with a characteristic length (between two neighbor peaks) of 1, 1/2 and 1/3 ship's length were plotted together with the corresponding squat. A strong interaction of the squat with the varying topography can be clearly observed, particularly at the characteristic length of the half ship's length. Looking more closely, on the contrary to the intuition, the maximum squat has not necessarily happened over the peaks. There is a phase shift between the bottom characteristics and the ship's squat. However, it should be pointed out, in such dynamic cases the effect of the ship's inertia has to be considered, i.e. to couple the equations of the vertical ship's motion into the computer program.