Abstract: For predicting the squat, sinkage, and trim of ships in shallow water a numerical method is developed. It is based on an extended shallow-water approximation using Boussinesq's equations for the far-field flow and a slender-body theory for the near-ship flow. It works in the subcritical, transcritical and supercritical speed range and covers all relevant effects associated with ship geometry and dynamics, varying water-depth and lateral restriction as well as the nonlinear and unsteady features of wave propagation.

　

 In comparison with standard analytical and empirical approximations it has been shown that the present method leads to a significantly better agreement with model experiments in the subcritical speed range and also to a much more satisfactory agreement in the transcritical and supercritical speed range. Additionally, it has been shown that the present method yields reasonable results for ships in shallow-water of infinite width and varying depth. Moreover, it has been found that there is a strong interaction between the ship's squat with the trackwise changed water-bottom, indicating a special attention should be paid for the ship operation over a varying topography.

　

 Due to the significant increase in size and speed of ships in recent years, problems caused by the ship's squat and trim in restricted water-depth and/or lateral extent have received more and more attention by ferry operators, naval architects, and port and waterway authorities, aiming to operate a ship without grounding hazard, to design a ship with less sinkage and trim,and to define a speed limit for safe operation.

　

 Physically, the ship's squat, which can be defined as the maximum sinkage along the ship's keel and corresponds the minimum clearance between water bottom and the ship's keel, depends on various parameters. Firstly, the squat depends on the basic features of the ship, such as ship's size and hull form, i.e. the geometrical factor. Secondly, the squat is a function of the ship's speed and of the resulting dynamic effects, such as the instantaneous wetted surface, i.e. the dynamical factor. Lastly, the squat is significantly influenced by the environmental conditions, such as water depth and/or lateral restriction, and current/wind/wave effects, i.e. the environmental factor.

　

 A considerable research effort has been devoted to the squat prediction. Various methods are developed for theoretical investigations and practical predictions.

　

 Based on the one-dimensional hydraulic theory for a channel flow, through the combination of the continuity equation and Bernoulli equation, the ship's squat as the mean sinkage of the ship can be analytically described as a function of the ship's speed and of the blockage factor, see e.g. Horn (1929) and Constantine (1960). The resulting formulae can be thus only used for a prediction of the ship's squat in a channel. Furthermore, due to the application of the steady Bernoulli equation, the hydraulic approximation works only in the subcritical and supercritical speed range. The squat at the transcritical speed can be not predicted by the hydraulic approximation.

　

 By using the technique of matched asymptotic expansions, where the far-field flow is approximated by means of linearized wave theory and the near-ship flow is described by a slender-body theory, an analytical formulation has been derived by Tuck (1966) for the prediction of sinkage and trim in shallow water of infinite width. A formulation for sinkage and trim in shallow water of finite width is then given by Tuck (1967). In comparison to the hydraulic approximation the steady linear theory does take account of the so-called secondary waves near the ship, thus enabling the inclusion of the trim effect on the squat. But it has a singularity as the depth Froude number closes to the critical value unity. Thus it yields unrealistic predictions in and near the transcritical speed range. An unsteady extension of this linear approximation has been done by Courlay (2002) for the prediction of the ship's squat in water of varying depth as well as at a transcritical speed. However, because the neglecting of the significant nonlinearity of waves in the transcritical speed range, it is still a restricted approach.

　

 A nonlinear extension of the technique of matched asymptotic expansions has been done by using the Kadomtsev-Petviashvili (KP) type equation for the far-field flow and a linear slender-body theory, see Mei & Choi (1987), or an extended slender-body theory, see Chen & Sharma (1992) for the near-ship flow. However, a practical restriction of the KP equation is that it is not valid for truly unsteady cases, caused, for instance, by varying topography along the ship's track. A more general shallow-water approximation is the application of equations of Boussinesq type, which are valid for almost arbitrarily unsteady cases. In Jiang (1998) a set of modified Boussinesq's equations, which are valid not only for long waves but also for waves of moderate length, was applied to compute waves as well as sinkage and trim of ships in shallow water, using an extended slender-body theory to approximate the near-ship flow.

　

 Based on experimental measurements in model and full scale, numerous empirical formulae are established for predictions of the ship's squat, see e.g. Barrass (1979) and Roemisch (2003). Commonly they are only valid in the subcritical speed range. As discussed by Fluegge & Uliczka (2001), most of the empirical formulae are not sufficient for the prediction of the squat of large containerships.

　

 The present paper focuses on an accurate numerical method of predicting the ship's squat in shallow-water. A shallow-water approximation based on extended Boussinesq's equations for the far-field flow and on a slender-body theory for the near-ship flow is applied to meet this challenge. This method works in the whole subcritical, transcritical and supercritical speed range and covers all relevant effects associated with ship dynamics, arbitrary bottom topographies as well as the nonlinear and unsteady features of wave propagation on the free surface. Theoretical treatment and numerical solution are summerized. Relevant results and experimental validations are discribed. Particularly, the effects of bottom topography on the ship's squat, sinkage and trim are discussed.

　

2.1 Coordinate System

　

 For describing the flow passing a ship moving in shallow water over a general topography, a right-handed earthbound coordinate system Oxyz is used. The origin O lies on the undisturbed water-plane. The x-axis points in the direction of ship's forward motion; the z-axis, vertically upwards; the sinkage s at the midship section (positive downward) and the trim θ (positive bow-down).

　

2.2 Boussinesq's Equations

　

 Considering water as incompressible and inviscid, the wave generation by ships in shallow water can be approximated by the well-established shallow-water wave theory, see e.g. Jiang (2001) for a review. Assuming that the water depth is small in comparison to the wave length and that the wave amplitude is small in comparison to the water depth, the wave field can be well described by shallow-water equations of Boussinesq type. In the present study, Boussinesq's equations based on the mean horizontal depth-averaged velocity for an uneven bottom, without corrections of the dispersion relation, are applied:

　

　

 which were first derived by Peregrine (1967). Herein, h(x,y) is the water depth, ζ(x,y,t) the wave elevation, μ(x,y,t) and v(x,y,t) the depth averaged velocity components in the x and y directions, respectively, t the time, and g the acceleration due to gravity. This set of nonlinear partial differential equations has to be solved numerically.

　

2.3 Conditions on Truncation Boundaries and on Vertical Channel Sidewalls

　

 On the truncation boundaries of the computational domain sufficiently far from the ship the Sommerfeld radiation condition

　

qt +σqx=0 or ql+σqy=0

　

 is applied, where q stands for each of the variables ζ, μ and ν, and σensures the local outgoing characteristic of the governing equations on the boundary in question, for instance, 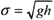ahead of the ship and 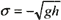behind the ship.

　

 On vertical channel sidewalls, if any, the condition of no-flux or, equivalently, perfect reflection holds.

　

2.4 Initial Conditions for the Computation

　

 In compliance with the unsteady nature of the flow, the ship is assumed to start from rest and accelerate uniformly to a final velocity like in a model towing tank. As may be expected, the final wave system is found to be influenced by the acceleration rate, especially in case of trackwise varying topography.

　

 This is because the waves caused by the accelerating ship with a rather arbitrarily assumed starting point can be reflected by the bottom topography and then interact with the waves generated by the ship at steady speed. However, a steady state could be reached in the subcritical and supercritical speed range.

　

2.5 Boundary Condition Resulting from an Approximation of the Near-Ship Flow

　

 By assumption of the slenderness of the ships considered, the general formulation of the depth-averaged mean transversal velocity resulting from the near-field approximation in Jiang (2001), reduces to

　

　

with the port-starboard mean values of the longitudinal velocity component

　

　

and of the wave elevation

　

　

 The hull sectional area is denoted by S(x), and the beam by B(x). For the far-field flow this is the boundary condition on the longitudinal ship-centerline (the mathematical dividing line between the near-field and the far-field).

　

2.6 Numerical Solution Method

　

 To solve this initial-boundary value problem governed by Boussinesq's equations, an implicit Crank-Nicolson scheme is implemented as usual. But it encounters some difficulties arising from the nonlinear terms and the linear high-order terms. The developed solution technique comprises:

2.7 Calculation of the Sinkage, Trim, and Squat

　

 For a ship of free heave and pitch, the resulting vertical force and pitch moment have to be vanish. kwise varying topography.

　

 Disregarding inertial effects believed to be small, the equilibrium conditions lead to the following pair linear algebraic equations:

　

　

where s(t) denotes the sinkage and θ(t) the trim at each time step. xbow and xsternare the longitudinal positions of the bow and stern, respectively. By using the usual nomenclatures in naval architecture:

　

　

inertia of waterplane, the explicit formulae can be given for determining the sinkage

　

　

These two formulae are identical with those derived by Tuck (1966) and Courlay (2002). The difference lies in the determination of the wave elevation ζ(x,t) along the waterline. In present study it is computed by using an nonlinear shallow-water Boussinesq's equations and there by means of a linear approximation.

　

According to the definition of the ship's squat as the maximum sinkage along the keel, the squat Sq can be defined by

　

　

where Lpp denotes the ship's length between perpendiculars.

 Based on an extensive study by Jiang (2001)a computer program BEShiWa, standing for Boussinesq's Equations for Ship Waves, has been developed with the following features: