Abstract: Considering the fact that nowadays more attention than ever is paid to the manoeuvring performance of ships, it is usually necessary to make reliable assertions concerning the manoeuvring behaviour and the dynamic yaw stability of a vessel in the early design stage.

 The paper gives a short overview of the measures that can be taken to demonstrate the manoeuvring quality of a new ship design. It further presents the state of the art regarding empirical regression formulas for linear sway and yaw damping coefficients. A regression approach developed by the author is given which focuses in more detail on the aft hull form of a ship. Furthermore, it is shown how the corresponding formulas can be used for a straightforward assessment of the manoeuvring quality.

　

 As long as no standardized ship types exist which are widely accepted, nearly each newbuilding is a new challenge for naval architects. This is due to the fact that almost all ship owners have very individual demands regarding their ships. Thereby the designer is often at the cross-roads of profitableness and safety. One main aspect of safety is the manoeuvring performance or controllability of a ship, which for a very long period was persistently ignored, Barr (1993). This has changed in the recent past. In 1993 the International Maritime Organization (IMO) passed tentative standards for the manoeuvring behaviour of ships, which are obligatory for several national authorities including the U.S. Coast Guard. Although IMO's interim standards are not the last word, they have given rise to a more intense concern regarding the phenomenon of manoeuvring behaviour.

　

 What measures are available for proving the manoeuvring quality of a new design? In principle three ways and means exist, the boon and bane of which are briefly discussed here.

　

 The traditional method is the model test, whereby it must be distinguished between force measurements on captive ship models and tests, e.g. zigzag manoeuvres, with the freely running ship model. Unfortunately manoeuvring model tests lie under some prejudices, namely that these are highly time consuming and therefore obligatorily expensive. Actually a relatively large effort is only necessary if the identification of a complete set of equations of motion with all linear and non-linear coefficients is required, for example as input for a shiphandling simulator. That also a shortened test program can be adequate is shown in Chapter 5.

　

 One alternative to model tests is the application of computational methods, nowadays propagated under the abbreviation CFD for Computational Fluid Dynamics. Although these methods have been rapidly improved during the last decade some reservations still remain. One ambitious aim is to estimate manoeuvring motions directly using unsteady CFD techniques. This means that the hydrodynamic forces are calculated using CFD codes and the ship response using the equations of motion, and both are to be solved simultaneously. In Germany first steps in this direction have already been made, e.g. Cura Hochbaum and Vogt (2002a). The present status is that the flow around the hull and the hull forces during steady drift and yaw motions are well represented by CFD methods based on the computation of the free surface viscous ship flow, e.g. Cura Hochbaum and Vogt (2002b). A certain disadvantage of nearly all known methods is that the inevitable preparations, e.g. grid set up, are relatively costly. Furthermore, the computer times needed to reach convergence are not small.

　

 A second, more economically efficient alternative is to use empirical regression formulas which have been presented by several authors for the four main linear sway and yaw damping coefficients of the equations of horizontal manoeuvring motions Y'v', Y'r, N'v and N'r. In the present paper a distinct proposal for different regression formulas is given. The basis for the novel approach is a paper presented by Clarke and Horn (1997).

　

　

 A very short review is given about those papers which are concerned with empirical regression formulas for the prime coefficients of the equations of horizontal motion. During the period of 1970 to 1993 these are:

　

 Wagner Smitt (1970/71) regressed nearly 30 data sets from complete hull PMM tests. Norrbin (1971) investigated a similar data base. In contrast to Wagner Smitt and Norrbin Inoue et al. (1981) considered also non-linear coefficients and various load conditions (ship on different draughts and trimmed). Clarke et al. (1983) and Oltmann (1992) additionally presented empirical formulas for the main added mass terms Y'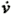, Y'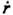, N' 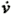and N'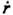. Kijima et al. (1993) and also Kose and Misiag (1993) mainly refer to the paper of Inoue et al. (1981) but included additional terms to improve the estimation accuracy.

　

 Common to nearly all papers mentioned so far is that the corresponding regression formulas were developed during a time when full-bodied bulk carriers and tankers were the dominating ship types on the main shipping routes. Furthermore, all authors used global hull parameters like CB, L/T, B/T, etc., and combinations of these.

　

 In the nineties it proved so conclusively that the aft body has a considerable influence on the manoeuvring performance and the dynamic yaw stability, respectively, of a ship. This holds in particular for container vessels whose aft hull forms were changed drastically in order to optimise the propulsion performance. To lend more weight to the aft body the following parameter, adopted from propulsion considerations, was introduced

　

　

where CWPa is the waterplane area coefficient and CPa is the prismatic coefficient of the aft half hull. Protagonists are

- Fujino(1996),

- Kose, Misiag and Xiong(1996), and

- Kijima, Nakiri and Furukawa(2000).

　

 Fujino (1996) and Kose et al. (1996) showed for a few, mainly full-bodied ships that new formulas using the parameter σa improve the accuracy of estimations. Kijima et al.. (2000) revert to the paper of Kijima et al. (1993) and again present approximate formulas for all linear and non-linear coefficients of their equations of horizontal motion. Equations for even keel and trimmed condition are given. The parameter σa is not treated merely but in several combinations with other hull parameters.

　

 HSVA's manoeuvring data base consists of more than 160 data sets for ships of various types (bulk carriers, container vessels, ferries, and passenger ships). Main sources are own manoeuvring tests performed with HSVA's Computerized Planar Motion Carriage (CPMC) in the towing Mode A and in the tracking Mode B, respectively. Also data from the open literature are incorporated. However, the latter are not useful because needed details of the aft hull body are usually not published. The only exception are the MarAd Systematic Series of Full-form Ship Models, Roseman (1987), which give detailed offset tables.

　

 Regarding the data from freely manoeuvring ship models (CPMC Mode B) it is customary practice at HSVA to use these data for the identification of a particular set of equations of motion, Oltmann (1978,1996). The belonging coefficients usually are not non-dimensional. However, provided the main added mass coefficients of sway and yaw Y'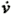, Y'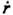, N' 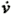and N' 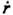are known a conversion into the commonly used non-dimensional coefficients can be accomplished. For this procedure usually the added mass regression formulas of Clarke et al.

　

 (1983) and Oltmann (1992) are used. A good indicator for the quality of these coefficients are the resultant rudder force coefficients Y'δ and N'δ whose ratio N'δ/Y'δ should be nearly -0.5. In case of obvious deviations a plausible correction of the dominating coefficients Y' 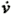and/or N' 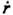can be introduced.