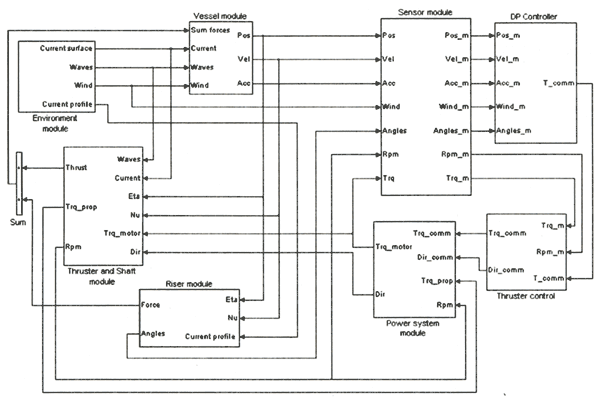
In Fig.8 the modules in the MCSim Simulink diagram for the present case are shown.

　

4.1 Objective

　

 The advantages of fully DP operated vessels are the ability to operate in deep-water, the flexibility to quickly establish position and leave location, and to start up in higher sea states than if a mooring system should be connected.

　

　

 In addition, there may be restrictions to deploy anchors due to already installed subsea structures on the seabed. For deep-water exploration and exploitation of hydrocarbons, DP operated vessels may be the only feasible solution. However, drilling operations at water depths less than 200-300m have normally been done with moored semi-submersibles or fixed structures. One reason for the skepticism towards applying DP operated vessels for drilling at shallow water depths, especially performing in hot oil and gas wells, has been the risk for drive-off initiated damages of the well head, in worst case resulting in an open well. Drive-off is an uncontrolled excursion of the vessel, which may occur due to a failure in the DP system. In this context position reference systems are examples of critical components that often cause problems. It is a class requirement that at least three of these systems are working with needed performance. Often only GNSS and HPR systems are available for measuring the rig position. Ideally, due to safety and availability reasons, there should be three different types of position reference systems, even though redundant systems are installed. This has been a motivation for looking for a third type of position reference system based on measurements of riser angle offsets at the bottom and the top of the risers. In [7] a method for the development of a riser angle position reference (RAPR) system is proposed.

　

 The most limiting operational factor in drilling is the tolerance for riser angle deviation relatively to the wellhead and at the top joint, see Fig.9. Ideally, the angle should be within ± 2 degrees. Deviations larger than 5-8 degrees may be fatal. Hence, in case of a drive-off the available time windows to decide and execute a controlled disconnect becomes more limited at shallow water compared to deep-water. On the other hand, more complex riser dynamics is appearing for increasing water depth. A further step in ensuring a safe and high performance DP operation is to actively take the riser angle offsets and bending stresses into account in the DP control strategy. This has been denoted as optimal setpoint chasing, for details confer [6].

　

　

 In the following, the use of a RAPR system in conjunction with the DP system is presented.

　

4.2 Class 3 DP Rig

　

 The semi-submersible (Fig. 3) is equipped with 4 azimuthing thrusters each capable of producing 1000kN, located at the corners of the two pontoons. The operational draught is 24m, the vessel mass at operational draught is 45000 ton, the length is 110m, and the breadth is 75m. The riser length used in the simulations is 1000m. The riser radius is 0.25m, the riser wall thickness is 0.025m, and the modulus of elasticity is E=2.1x10⁸ Pa. The top tension is 2500Pa, and the tension of the lower part is 1200Pa. In the simulation the riser is divided into ten elements.

　

4.3 Vessel Model

　

 The nonlinear 6 DOF body-fixed coupled equations of the low-frequency (LF) motions in surge, sway, heave, roll, pitch and yaw are written as defined in [5] according to

　

　

 The effect of current is included in the 6 dimensional relative velocity vector vr ・τthr is the 6-dimensional control vector consisting of forces and moments produced by the thruster system. τwind and τwave2 are the 6-dimensional wind and second order wave load vectors, respectively. τext is the 6-dimensional load vector, in this case due to the riser.

　

 The coupled equations of wave-frequency (WF) motions in surge, sway, heave, roll, pitch and yaw are assumed to be linear, and can in the reference-parallel frame [5-6] be formulated as

　

　

 τwave1 is the 6-dimensional excitation vector, which will be modified for varying vessel heading relative to the incident wave direction. The WF motions may also be found by time realization of transfer functions. For detailed explanations of (1) and (2), see [5-6].

　

 Assuming small roll and pitch motions, the Earth-fixed motion vector can be found by the kinematics relation [5]

　

　

4.4 Riser Module

　

 Considering low frequency riser motion, the driving excitation mechanism is due to forced motions caused by the surface vessel at the upper end of the riser. The direct hydrodynamic loading from waves on the riser can then be neglected, but forces from current and riser motions must be considered. The sub-vectors of the riser elements are assembled into a total nodal riser displacement vector (containing both displacements and rotations), designated by r. The dynamic equilibrium equation can then be written [5-6] according to

　

　

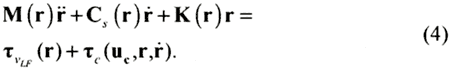
 The mass matrix M, structural damping matrix Cs, and stiffness matrix K are all considered functions of the deformed configuration found from the displacements. Two loading terms τvLF and τc are present, one containing contributions from LF vessel motions and the other with loads from the current velocity vector uc and the riser velocity vector 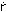. A generally applied simplification of (4) is to neglect the two dynamic terms related to inertia and damping forces. The model is then said to be quasi-static, meaning that the response model is static, but external loads are calculated by taking the riser motions into account. Such models will yield acceptable accuracy for shallow water applications. Dynamic effects will become more important in deep-water, since the lowest eigenfrequency of the riser may approach the LF motion regime. An even further simplification of (4) is to neglect the influence from riser velocity in the load caused by the current. This type of model has been applied in the present simulation study.

　

4.5 DP System

　

 The DP system consists of various internal modules for signal processing, output controller and thruster allocation. The nonlinear horizontal-plane positioning feedback controller is formulated as

　

　

 where e is the 3-dimensional position and heading deviation vector, is the 3-dimensional velocity deviation vector, and z is the 3-dimensional integrator states defined as

　

　

 ηd the 3-dimensional vector defining the desired Earth-fixed position and heading co-ordinates.

　

　

are the estimated position and velocity vectors computed by a nonlinear observer. Kp,Kp3,Kd and Ki are the 3x3 non-negative controller gain matrices found by appropriate control synthesis methods. In addition a wind feedforward control action and a roll-pitch damping control action could be added as proposed in [6].