As previously discussed, the framework is implemented in the C++ language and the capabilities of the language are fully utilized. The main framework classes are all defined within the context of the ofsmvd namespace. Namespaces are supported by the language to help alleviate the problems associated with collisions between the names of functions and classes. The additional classes that perform specific numerical methods for Solvers and specific models for Vessels exist in their own namespace, ofsmvdutility.

　

 The framework also supports several different paradigms for performing time stepping. When a Solver is created it is given its own time step value. The time steps do not need to be identical for all Systems. When the simulation is initialized by a call the Environment's InitializeEnvironment method, a start time is provided. Each Solver maintains its own current time and the start time is passed to each Solver in the Environment. Performing a time step for the whole simulation or an individual Solver has different forms. The Environment has four different flavors of the Step member function to support some of the different forms of time stepping. One of these simply iterates over all of the Solvers and instructs each one to advance by its own time step. At the end of the step, the Solvers are not necessarily synchronized. By default, when each Solver is advanced, a post step member function is called for its related Systems, however, this can be delayed until all Solvers have taken a step. Another time stepping method advances all Solvers to the same point in time, with the same post step functionality. If needed, a single specific Solver could be advanced using its own time step or advanced to a specific point in time. In these two cases, the post step functions for the associated Systems are executed immediately after the step.

　

 When a Solver makes a time step, it must access the starting values of each state and perform some mathematical operations on those values. These mathematical operations can be performed on each individual state value of on an entire vector of the state values. A trade-off is made here between internal complexity and efficiency. The C++ language defines a class, named valarray, which is intended to provide highly optimized numerical operations on vectors of numeric values. So instead of performing mathematical operations on each individual state value, a valarray is constructed from all of the state values associated with the Solver. The valarray is then used to perform the mathematical operations on a whole vector. This has the added benefit of making the notation concise for the implementation of Solver classes.

　

 At the end of a time step, the Solver class checks with its associated Systems to validate the step. This offers the possibility of detecting and responding to collisions. If required, the time step can be "rolled back" and redone to some intermediate point. At that point, forces due to impact or contact could be determined and applied. From there, the time step is allowed to be completed. Another use could be high precision control. For example, when performing a zig-zag maneuver the rudder position is changed when the heading angle reaches a particular value. If that angle is exceeded in mid step, the step can be subdivided to the point where the heading reaches exactly the required angle. Another example is the application of mooring line forces, where the line goes from slack to tight across a time step. The initial time step could be relatively large while slack, and adjusted to a smaller value at the point when the line becomes tight and initially elastic.

　

 A basic 2^nd order system can be represented by the equation,

　

　

 where ξ is the linear damping coefficient and ωn is the natural frequency of the system. This type of equation could represent a spring-mass-damper system or the rolling of a ship. Here we will assume the later and take θ as roll angle. This equation can be written as a system of two first order equations with 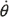and θ as the states. The complete listing of the program source code for this example is given in Table 2.

　

 To represent this system using the framework, a new class, named RollVessel, which inherits from the Vessel class, is defined. This class contains two reference-counted State objects, one for each of the mathematical states. These are dynamically created in the constructor of the RollVessel class. Within the RollVessel initialization member function, initial conditions for the States are provided. The Evaluate member function of RollVessel is where the equations of motion are evaluated to provide the States their derivative values. For the purposes of this example, one reference-counted Value object is declared as a property of the RollVessel. This Value object will be used to extract the value of the roll angle at each time step which can then be accessed by the application. The UpdateSystem member function of the RollVessel is where the roll angle is extracted from the corresponding State object and provided to the Value object. Two other member function are also defined, GetStates and GetValues. These return a list of the State and Value objects, respectively, maintained by the Roll Vessel.

　

 The application main program function then needs to declare an Environment object, dynamically allocate a Solver object and a RollVessel object. Here, the Euler solver provided by the framework is used. Prior to the loop over time, where the equations of motion are integrated, the Environment is instructed to perform initialization, which in turn results in the RollVessel object being initialized. Within the loop, the Value objects that are known by the Environment are retrieved (in this case, one Value), and the values are printed. The loop is terminated when the current simulation time exceeds the desired maximum. Note the try block that encompasses the creation and use of the framework defined and inherited objects. Any exception that might occur will be trapped by the try block and control passed to the subsequent catch blocks in the order which they appear. The first catch block will handle framework exception types (OfsmvdException). If the exception type is not an OfsmvdException, the next catch block will be attempted. In this case, the second catch block will trap all exceptions (that have not been previously trapped). Any OfsmvdException will result in a printed message that explains the error condition while all others result in a printed message indicating that an unknown exception occurred.

　

 It is worth noting that for this example, no Effector objects are defined for the RollVessel. Hence, there is no need to obtain forces and moments. There is also no environmental conditions declared or used, since they are not needed for the example. This illustrates that only those parts of the framework which are required to model and solve a problem, need be used. The framework features that are not needed for a particular problem do not interfere with expressing the problem in program source code.

　

　

 The abstract nature of the framework offers many potential benefits to simulation software developers. Since the fundamental relationships and behaviors that are necessary to perform a simulation are defined by the framework, the metaphorical wheel need not be re-invented. The task of software maintenance and extension is also made easier by using the framework.

　

 Organizations that are involved with the development of marine simulation systems will undoubtedly have a large amount of legacy code, usually in FORTRAN. It is possible to "wrap" such legacy code in objects that are part of the hierarchy of framework classes. Such objects could coexist with a variety of other object types.

　

 The forces and moments that are applied to Vessels can be determined in any way, using any method - empiricism, interpolation of test data, or computational fluid dynamics (CFD), for example. If properly handled, the components that exert forces and moments (Effectors) could be interchanged with components utilizing other methodologies, or components developed by others. This capability offers the possibility of promoting the exchange of models and techniques. This would undoubtedly enhance the ability of such models and techniques to be validated and improved by others.

　

 This paper has presented the basic concepts behind the OFSMVD framework and some of its inner workings. It has been shown that the framework is comprehensive in its coverage and efficient in its implementation. It has also been shown that the architecture is flexible enough to allow the user to develop applications that use nearly any idiom imaginable for performing simulations, and that the possibilities are limited only by imagination.

　

 It is hoped that the OFSMVD framework will be embraced by the marine simulation community and those who develop marine simulations. The framework could become the basis for a standardized methodology for the exchange of models and model data. By placing the framework source code and documentation in the public domain this result will hopefully be enabled.

　

[1] Kopp, Paul J., "Mathematical Model for a Real Time Ship Maneuvering, Stationkeeping, and Seakeeping Training Simulator", CRDKNSWC-HD-1427-01, September 1993.

[2] Kopp, Paul J., "Mathematical Model for MANSIM Version 2: A Surface Ship Maneuvering, Stationkeeping, and Seakeeping Simulator Computer Program", CRDKNSWC/HD- 1427-02, October 1996.

[3] Kopp, Paul J., "Mathematical Model for MANSIM Version 3: A Surface Ship Maneuvering, Stationkeeping, and Seakeeping Simulator Computer Program", NSWCCD-50-TR-2000/009, January 2000.

[4] "Conning Officer Virtual Environment: Final Report", BBN Technologies, 2002.

[5] Roberts, Bruce, "COVE-A Shiphandling Trainer with an Attitude", Proceedings of the Interservice/Industry Training, Simulation and Education Conference, 2001.

[6] C++ Language Standard,

[7] Lee, Han-Jin, Chang-Min Lee, Gyeong-Joong Lee, and In-Young Gong, "Development of Shiphandling Simulator by Object Oriented Software Design", International Conference on Marine Simulation and Ship Maneuvering - MARSIM 2000, May 2000.

[8] Fayad, Mohamed E., Douglas C. Schmidt, Ralph E. Johnson, "Building Application Frameworks - Object Oriented Foundations of Framework Design", Wiley Computer Publishing, 1999.

[9] Muller, Pierre-Alain, "Instant UML", Wrox Press, 1997.

[10]Press, William H., William T. Vetterling, Saul A. Teukolsky, Brian P. Flannery, "Numerical Recipes in C++: The Art of Scientific Computing", 2^nd Edition, Cambridge University Press, 2002.

　

 Mr. Kopp has been a naval architect with the Naval Surface Warfare Center, Seakeeping Department, located in West Bethesda, Maryland, for twenty years He has been involved with dozens of projects relating to ship model testing, marine simulation, static and dynamic stability analysis, seakeeping performance predication, and software development. Mr. Kopp received a BS degree in Naval Architecture and Marine Engineering from the University of Michigan in 1984. In 1991, he received MS degree in Naval Architecture and Marine Engineering from the University of Michigan. Mr. Kopp is an associate member of the Society of Naval Architects and Marine Engineers and is a member of the Society's T&R Panel H-10 (Ship Controllability).