|
3. DERIVATIVE PREDICTION
The objective was to formulate derivative prediction tools which take into account both the effect of pod units and the change in hull-form caused by their introduction. The hull-derivatives are estimated from semi-empirical methods while the control force is obtained through empirical equations.
3.1 Hull-derivative Estimation
Several papers have proposed semi-empirical equations in the past [11-14], though not specifically investigating the effect of introducing pod units. In general, both the proposed and the existing methods start by predicting the forces acting on a flat plate of equivalent draught length ratio. The change in this value due to form is then estimated from the principal ratios and coefficients based on a multi-variant analysis of similar ship forms and corresponding captive test results. Previously, methods have taken into account principal ratios and coefficients but fail to account for variations in the aft body form; often found to contribute significantly.
To address this problem a multi-variant analysis was performed on a data base of 64 captive model test results covering a wide range of hull forms; Table 1. As usual, the principal ratios and coefficient are used but the subtlety of aft body form is now accounted for by the inclusion of the aft body shape parameter, σα. Where σα a function of the aft body water plane and prismatic coefficients, Eq.(1).
3.2 Velocity Derivatives
Multi-variable linear regression was used to examine the variation in the collected data between the descriptive parameters and the measured derivatives.
Table 1 Derivatives database range
| Variable |
Minimum |
Maximum |
| B/T |
2.068 |
5.724 |
| B/L |
0.118 |
0.250 |
| T/L |
0.025 |
0.069 |
| CB |
0.562 |
0.850 |
| σa |
0.002 |
0.940 |
|
The decision to retain a given predictor variable was based on its attained t-statistic where the t-statistic for all retained variables is above 5% significance. The constant term in each case was not forced but, as seen in Eq.(2) to Eq.(5) come close to the value expected from potential flow for a flat plate [11].
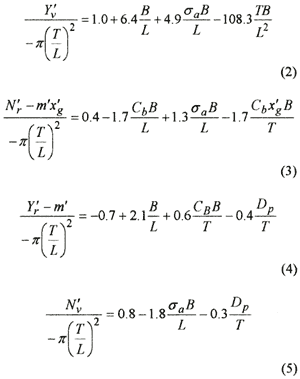
Using the four OPTIPOD designs, the velocity derivatives have been estimated with both the proposed semi-empirical equations and with equations from the existing literature [11-14]. The estimated values are then compared with the results from the captive model tests. The mean error between estimated and measured derivatives of all designs is calculated and shown in Fig. 5. Clearly, the proposed equations [15] show significant improvement over existing methods. Notably, the derivative for yawing moment with respect to yawing rate gives much improved results and is thought to be the most significant hull form term [16]. Though based on, and equally applicable to, conventional hull shapes the proposed model predicts the derivatives for the OPTIPOD hull-forms very well.
Fig. 5. Comparison of Derivative Estimation Models
|