Abstract: Based on analyzing wave scales and wave spectrums, the paper discretizes adaptively wave spectrums to different single frequency, the data are applied in simulation model for simulating irregular long crest wave. Unique mesh model and texture mapping technology are also adopted to simulate wave in real-time.

　

 Natural phenomenon simulation is considered a challenging field of computer graphics. Many scholars have tried various ways to simulate ocean which covers more than 70 percent surfaces of earth. Turner Whitted is the first scholar who tried to simulate wave. He used ray tracing to simulate reflection wave in small pool. Because the calculating speed of ray tracing is slower, it's difficult to use this method in real-time simulation. In 1985, Bump Mapping technology was used by Ken Perlin^[1] to simulate bird's eye-view of sea. But the approach can not show the contour of wave. In 1986, wave-shape function and phase function were adopted by Darwyn R. Peachey^[2] to describe sea, the approach makes the simulation of different waves easier. Alain Fournier^[3] applied trochoid to ocean surface presentation. All of these approaches are based on "shape-similar", the simulated waves can not match with wave scales and wave spectrums. How to consider both wave spectrums and wave scales during wave generating in visual system? How to implement wave generating algorithm in real-time? The paper will present an approach to simulate irregular long crest wave in real-time which can match with specified wave spectrum.

　

 Wave is a very complicated natural phenomenon which is irregular and non-repeatable in time and space. But the statistic characteristic of full developed wave is stable and not change with time, so this kind of wave can be considered as a stable random process. The mathematical expectation of this random process m=0, variance is:

　

　

 Normally significant wave height 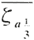denotes the wave height measured by observation through human eyes, the relation of significant wave height and standard deviation is:

　

　

 The relation of wave spectrum density and amplitude is:

　

　

 When one wave consists of infinite single waves, ωi ∈(0, ∞), we have:

　

　

 From the above formula we can know that the density of wave spectrum Sζ(ω) is in the direct proportion of energy of wave unit.

　According to the relation formula of variance and amplitude, the following formula denotes the relation of variance spectrum density:

　

　

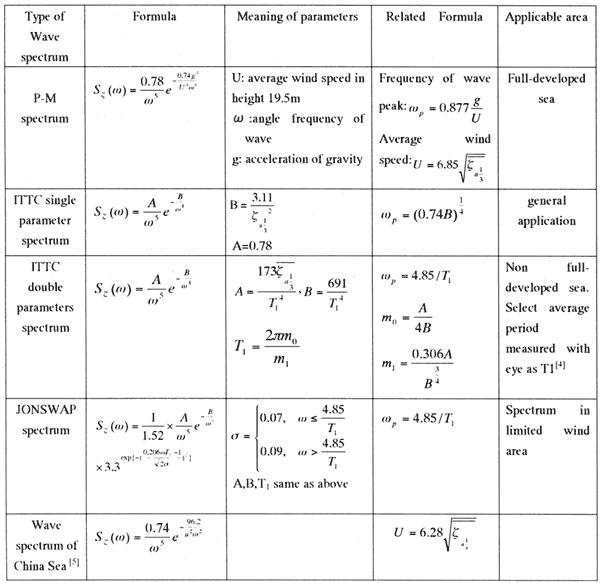
 If he spectrum density Sζ(ω) of sea wave has known, the variance σζ² of irregular wave can be deduced, so the significant height of wave 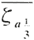of irregular wave can be calculated. Scholars majoring in ocean and ship-building summarize several formulas for calculating wave spectrum according to a mass of of observing data (Listed in Table 1).