|
7・5・7 電圧, 電流の有効分と無効分
交流回路において, 電圧と電流の間に位相差があるときは, 図7・52(a)のように電圧E〔V〕を電流I〔A〕の同相の成分Ewと
の位相差をもつErとに分解し, また, 図7・52(b)のように電流 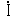 〔A〕を電圧  〔V〕の同相の成分 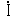 wと
の位相差をもつ 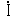 rとに分解して考えると便利な場合がある。
図7・52
この関係を式で次のように表す。
Ew=E cosθ〔V〕, Er=E sinθ〔V〕・・・(7・65)
Iw=I cosθ〔A〕, Ir=I sinθ〔A〕・・・(7・66)
ここで, Ewは電圧有効分, Erは電圧無効分, Iwは電流有効分Irは電流無効分である。これらの式を使って電力と無効電力を示せば次のようになる。
電力=EI cosθ=E(I cosθ)又は=I(E cosθ)
無効電力=EI sinθ=E(I sinθ)又は=I(E sinθ)
(1)電圧の瞬時値e=Em sinωt, 電流の瞬時値 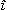 =Im sin(ωt-90°)の電力P(瞬時値)を計算せよ。 (2)電圧の瞬時値e=Em sinωt, 電流の瞬時値 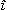 =Im sin(ωt-θ)の電力P(瞬時値)を計算せよ。 (3)電気角はどんな角か説明せよ。
(4)交流発電機の極数, 周波数, 回転数毎分の関係式を示せ。
(5)位相について記せ。
(6)電圧と電流の実効値と最大値との関係を示せ。
(7)XLとXCを説明せよ。
(8)静電容量C1, C2, C3の和
をCの形で表わせ。
(9)R, Lの直列回路を計算し, V, I, Zの値を示せ。
(10)R, L, Cの直列回路を計算し, V, I, Zの値を示せ。
(11)抵抗R〔Ω〕のR1, R2, R3が何れも並列の場合の合成抵抗Rを計算せよ。
(12)
の式でXLの合成リアクタンスを計算せよ。
(13)R, L, Cの並列回路を計算し, IとZの値を示せ。
(14)R, Lの直列回路における電力を計算せよ。
(15)力率とはどんな意味か説明せよ。
(16)電力と皮相電力と無効電力の関係を示せ。
(17)電流の有効分と無効分を示せ。
(18)
上図に示す回路の皮相電力, 〔VA〕, 力率〔%〕及び電力〔W〕を求む。
|