|
10. 付録、理工学及び求積関係公式
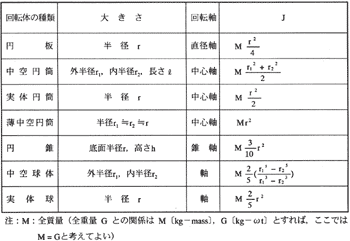
10・1・1 慣性モーメント〔J〕とはずみ車効果〔GD2〕
上図において回転軸Aからr〔m〕だけ離れた所にm〔kg〕の質点が角速度ω〔rad/s〕で回転しているとき、その周辺速度
V=2πrn=rωであるから、質点のもつ運動エネルギーW〔J=1Nm〕は次の式で表される。
ここで J=mr2〔kgm2〕なるJをm質点のこの軸に対する慣性モーメントという。(単位のJ(ジュール)とは違う)
実際では、回転物体はいろいろの形状をもって回転軸のまわりを回転しているから、この考えを拡張して、全質量をM〔kg−mass〕、回転体の半径R〔m〕の所に全質量が集まったと考えれば、上式のJは次のようになる。
J=MR2〔kgm2〕 R:回転体半径〔m〕、D:回転体直径〔m〕
かつ D=2R、M=G〔kg−ωt〕とすれば
| (拡大画面:12KB) |
 |
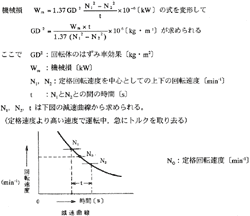
この(3)式の運動エネルギー式から次のことが判断できる。
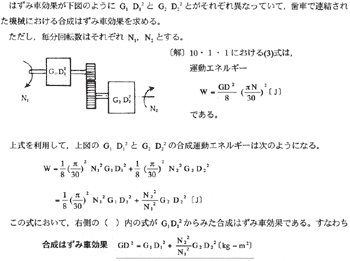
はずみ車効果のGD2は物体の固有の値で、これが大きいとWが大幅に変化してもN(毎分回転数)の変化は少ない。すなわち、運動エネルギーWが減速する場合はGD2がエネルギーを放出し、反対に増進する場合はエネルギーを吸収し、次の減速の場合にそなえる役目をするので、はずみ車効果すなわち、GD2が大きいものほど速度変化の少ないことがわかる。
| (拡大画面:26KB) |
 |
| (拡大画面:25KB) |
 |
| (拡大画面:58KB) |
 |
| (拡大画面:34KB) |
 |
| P=ps |
P:全圧力(全張力) |
p:圧力(張力)の強さ |
| |
s:全面積 |
|
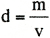 |
m:質量 |
v:体積 |
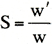 |
w':物質の質量 |
w:4℃の水の質量 |
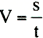 |
s:運動した距離 |
t:運動に要した時間 |
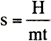 |
H:熱量 |
m:質量 |
t:温度差 |
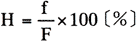 |
f:空気中の水蒸気圧 |
| |
F:その温度における水蒸気の最大圧力 |
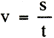 |
s:距離 |
t:時間 |
| v=nλ |
λ:音の波長 |
n:振動数 |
| v=4nl |
l:共鳴箱の長さ |
|
| B=n1−n2 |
B:うなりの数 |
n1:1音の振動数 |
| |
n2:別音の振動数 |
|
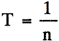 |
T:波の周期 |
t:単位時間に振動する数 |
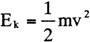 |
G:重力の加速度 |
h:物体の位置(2点間の高さ) |
| Ep=mGh |
G:重力の加速度 |
h:物体の位置(2点間の高さ) |
10・2・4 台形の面積=(上底+下底)×高さ÷2
10・2・7 球の表面積=4π×(半径) 2=π×(直径) 2
10・2・8 直角筒(直円筒)の側面積=底面の周×高さ
10・2・12 角筒(円錐)の体積=底面積×高さ÷3
| 大文字 |
小文字 |
読み方 |
通常の用途 |
| Α |
α |
アルファ |
角度、係数、面積 |
| Β |
β |
ベータ |
角度、係数 |
| Γ |
γ |
ガンマ |
角度、比重、導電率 |
| Δ |
δ |
デルタ |
微小変化、密度 |
| Ε |
ε |
イプシロン |
(小文字)自然対数の底=2.71828、微小量、誘電率 |
| Ζ |
ζ |
ツェータ(ジータ) |
(大文字)インピーダンス、垂直軸 |
| Η |
η |
イータ |
(小文字)効率、ヒステリシス係数 |
| Θ |
θ |
シータ |
角度、位相差、時定数 |
| Ι |
ι |
イオタ |
|
| Κ |
κ |
カッパ |
(小文字)誘電率 |
| Λ |
λ |
ラムダ |
(小文字)誘電率、波長 |
| Μ |
μ |
ミュー |
(小文字)誘電率、真空管増幅率、マイクロの略 |
| Ν |
ν |
ニュー |
(小文字)磁気抵抗率 |
| Ξ |
ξ |
クザイ(クシー) |
|
| Ο |
ο |
オミクロン |
|
| Π |
π |
パイ |
円周率(3.14159・・・)、角度 |
| Ρ |
ρ |
ロー |
抵抗率 |
| Σ |
σ |
シグマ |
(大文字)数の和を示す、(小文字)導電率 |
| Τ |
τ |
タウ |
時定数、位相の時間的ずれ、トルク |
| Υ |
υ |
ウプシロン |
|
| Φ |
φ |
フアイ |
(大文字)磁束、(大文字)角度、誘電束 |
| Χ |
χ |
カイ(キー) |
(大文字)リアクタンス |
| Ψ |
ψ |
プサイ |
誘電束、位相差、角速度 |
| Ω |
ω |
オメガ |
(大文字)抵抗の単位記号、(小文字)角速度−2πf |
|
|