図3・3(a)は直流電圧計の実態結線図で、図3・3(b)はその接続図を示したものである。mは可動コイル、Rは倍率器といい、直列抵抗であって電圧計の指針が最大目盛を指すような位置にその値を選定する。
この倍率器の抵抗材料には、固有抵抗が高く温度係数の小である
マンガニンという抵抗金属を用いる。普通この倍率器は計器の外部に装置する。
図3・4において、3・4・1(2)のNSの磁極の代りにF1、F2の固定コイルを用いその中間に可動コイルmをおく。図3・4のように、電流iを流せば固定コイルの磁界と可動コイルmとの間に電磁力が生じこれはi 2に比例する電流力が作用する。そして、可動コイルmに駆動トルクが生じ、これに連結されている指針が動く。
図3・4
今、i を交流の瞬時値電流、Iを交流の実効値電流とする。
瞬時トルク τ=κi 2ここでκ比例定数
平均トルク Taυ=(τの1周期間の平均)
=κ( i の1周期間の平均)=κI2
Taυ=κ1I2・・・(3・5)
この関係を図示すれば図3・5のようになる。
図3・5
このように、電流(又は電圧)の2乗に比例する力を利用する計器は、交流用計器として利用される。
| (拡大画面:21KB) |
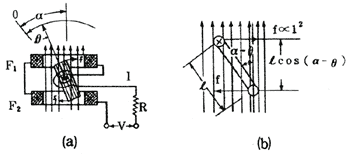 |
図3・6
図3・6(a)(b)において、被測電圧Vを計器端子にあたえれば電流Iが流れ、固定コイルF1F2と可動コイルmとの間にI2に比例する電力が生じ、mに駆動トルクができることは3・5・1項で述べた。
今、Fの磁界の方向と指針の零位との間の角をα約45°とし指針の偏れをθとすれば、mに働く電流力fはI2に比例する。mに作用する駆動トルクTdとし、制御トルクTcはθに比例する。
よって、 Td=κ11I2cos(α−θ) Tc=κ2θ
Td=Tcとして力が釣り合うから
κ11I2cos(α−θ)=κ2θ
故に、I2=κ×θ/cos(α−θ)又はθ∝I2cos(α−θ)・・・(3・6)
しかるにI∝E、故にθ∝E2cos(α−θ)・・・(3・7)
となり目盛盤には、直接被測電圧Vを目盛ることができる。
しかし、この目盛は、不平等目盛で中央が幅広く、零位に近づくにしたがって幅は狭くなる。
なお、直列抵抗Rを用いた理由は、合成温度係数を小にすることと、直流又は交流に用いても共に同一の確度を得るためである。普通この計器の動作電流は50〜100〔mA〕である。
図3・7
0.25〔A〕位までの電流であれば、固定コイルFと可動コイルmとを直列にして電流計にすることができる。しかし、これ以上の電流になれば、うず巻きばねの制御装置では無理であるから、図3・7のように可動コイルmには被測電流に比例する小電流を分流させて電流計とする。
図3・7は、5〔A〕用の電流計を示したものである。F及びmには被測電流Iに比例する電流I1、及びI2が流れ、可動コイルmに作用する電流力はI1×I2したがって、I2に比例する。よって、(3・6)式によって目盛上には直接被測電流Iを目盛することができる。