|
6・3・1・3 海上の遠距離におけるレーダー電波伝搬方程式
前述のように、海面が地球表面に沿って湾曲していることを考慮しなければならないような遠距離の伝搬の場合は、 図6・6のように、海面上の反射点における水平線を引いて考え、レーダー・アンテナ及び物標の高さのうち、その水平線より上の部分をそれぞれAs及びAeとする。そして、 (6・5)式のHs、Heの代りにAs、Aeを入れれば、 (6・6)式が成り立つ。
| (拡大画面:29KB) |
 |
図6・6 海上遠距離伝搬図
ただし、
As=Hs−(R2×Hs2)/{2×Re×(Hs+He)2}
Ae=He−(R2×He2)/{2×Re×(Hs+He)2}
である。このAs、Aeは、付録2に示すような略算によっている。
以上のレーダー電波伝搬方程式は、物標がレーダーリフレクタのような点物標で、海面上のある高さに掲げられている場合は実測値と計算値が非常によく合致することが確かめられた。
物標が船のような場合は、種々の値のレーダー反射断面積を持った点物標が海面上にそれぞれの高さに分布している複合体として計算すれば、わりあいに実測値と合うことも分かっている。この計算は複雑であるので、船の総トン数に応じた等価的なレーダー反射断面積σと、有効高Heを与えて点物標とみなして計算することが考えられる。
図6・7は船の総トン数対レーダー反射断面積σ(m2)のグラフであり、
図6・8は船の総トン数対有効高He(m)のグラフである。
| (拡大画面:36KB) |
 |
図6・7 船の総トン数対σ(m2)
| (拡大画面:42KB) |
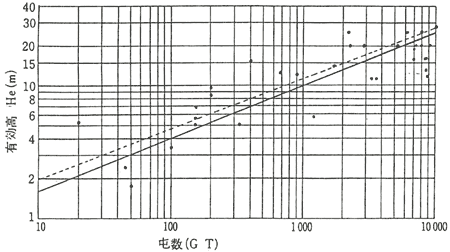 |
図6・8 船の総トン数対He(m)
これらの推定曲線は、トン数の分かった船の反射強度を追跡測定して、R4に反比例する曲線部のレベルからσを計算し、反射強度が急激に下がる曲線部分との変曲点の距離からHeを計算して、その船のσとHeとして両対数グラフ上にプロットすることによっている。そしてこのグラフ上にトン数の異なる多くの船について測定した値をプロットして、最小自乗法によって得られた曲線に最も近くて判りやすい曲線から得られたものである。
|