|
8・2 照明の基礎
単位時間にある面を通過する光の量を光束〔記号F〕という。
光束の単位をルーメン〔単位記号lm〕という。
光束の時間積分を光量〔Q〕といい単位にルーメン時〔lm・h〕又はルーメン秒〔lm・s〕などを用いる。
単位面積当りの入射光束を照度〔記号E〕といい、照度の単位をルクス〔単位記号lx〕という。
照度 E=F/A〔lx〕
F:光束〔lm〕 A:入射光束の面積〔m2〕
注:照度の時間積分を露出〔Ex〕といい単位にはルクス秒〔lx・s〕又はホト秒〔phot・s〕
などを用いる。
光源からの光の強さの程度を示すのが光度で、単位立体角当りに発散される光束が光度である。光度記号はIで示し単位にはカンデラ〔単位記号cd〕を用いる。
光度 I=F/ω〔cd〕
ω:立体角〔ステラジアンsr〕
注:立体角ステアラジン〔sr〕について
上図において、ある点に対する空間の拡がりを表すのに立体角を用いる。すい体の含む立体角がω〔sr〕ということは、すい体の頂点Oを中心とし、任意の長さr〔m〕を半径とする球を描いたとき、すい体がこの球から切り取る表面積をs〔m2〕とすると
ω=s/r2〔sr〕で与えられる
したがって、半径r〔m〕の球ならその表面積はs=4πr2〔m2〕である。
半球ならs=2πr2〔m2〕であるから、次のようになる。
| (拡大画面:8KB) |
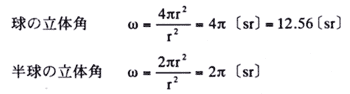 |
また上図の球帽なる、その立体角は次の式で表す。
ω=2π(1−cosθ)〔sr〕
以上のことから光束の単位の1〔lm〕は1〔cd〕の一様な光度の点光源が立体角1〔sr〕内に発散する光束といえる。
〔例題〕100〔w〕の白熱電球の光束は、1,500〔lm〕である。均等点光源とみなした場合、その光度はおよそ何〔cd〕か。
(注)1〔cd〕=4π〔lm〕=12.56〔lm〕(均等点光源の場合)
昭和21年改訂の白熱タングステン電球標準規程では10lm=1cと定めた。ここでcはカンドルと称し、1c=1.0067〔cd〕である。以上参考のため記す。
光源のまぶしさをいい発光面を見たときの明るさの程度を表すのが輝度(記号B又はL)である。いまS〔m2〕の発光面からF〔lm〕の光束を発散し、その面に垂直方向の光度がI〔cd〕ならば
輝度 B=I/S〔cd/m2〕
輝度の単位にスチルブ〔単位記号sb〕という場合は1〔cm2〕あたり1〔cd〕の輝度である。また1〔m2〕あたり1〔cd〕の場合はカンデラ毎平方メートルといい〔単位記号cd/m2〕、これをニト〔単位記号nt〕ともいう。
例えば上図のようなガラス面に光束F〔lm〕が入射すると、その一部のFr〔lm〕が反射し、また一部Ftが透過し、残りのFaはガラス内部に吸収される性質がある。よって、それぞれの光束Fr、Ft、Faの入射光束のFに対する比を次のように定義している。
| (拡大画面:8KB) |
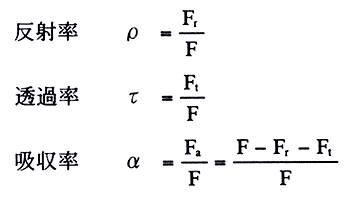 |
ここでF=Fr+Ft+Faの関係から
ρ+τ+α=1である。
以上述べた反射率、透過率、吸収率は物質によってそれらの値は異なるばかりでなく光源の波長及び反射率も投射角などによって変わるものであるが、ここでは一応100〔W〕昼光電球の光に対する場合につき次に示す。
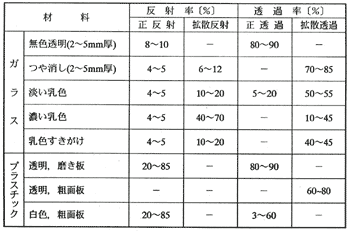
(1)ガラス及びプラスチック材料の反射率、透過率
| (拡大画面:31KB) |
 |
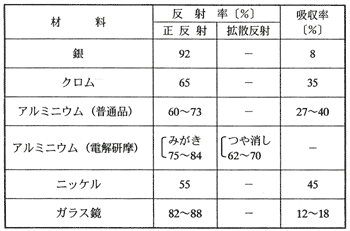
(2)金属材料の反射率・吸収率
| (拡大画面:25KB) |
 |
注:1. 正反射とは入射角と反射角とが等しい場合のとき
2. 拡散反射とは粗面で乱反射が行われて光が散乱する場合のとき
3. 正透過とはガラスや紙などを光が透過するとき光が拡散しない場合のとき
4. 拡散透過とは各方向に光が拡散しながら透過する場合のとき
〔例題〕すべての方向の光度が一様に1,000〔cd〕の光源がある。これを直径40〔cm〕の完全拡散性球形グローブの中心に点じたとき、その輝きは1〔cm2〕当り0.56〔cd〕となった。このグローブの透過率は何〔%〕であるか。
ただし、グローブ内面の反射は無視するものとする。
〔解〕グローブは完全拡散性であって内面の反射を無視すれば、グローブの光度は光源光度に透過率を乗じたものである。
| (拡大画面:8KB) |
 |
光を発散している面の明るさの程度を表すのが光束発散度〔記号M又はR〕で、これは光を受けている面の性質に大いに関係する。この単位は1〔m2〕あたり1(lm〕の光束を発散しているときの光束発散度で単位記号は〔lm/m2又はラドルクスrlx〕である。
| 一般の光束発散度 |
M=F/S〔lm/m2又はrlx〕 |
F:光束〔lm〕 |
S:面積〔m2〕 |
| 反射光の場合 |
M=ρE〔lm/m2又はrlx〕 |
ρ:反射率 |
E:照度〔lx〕 |
| 透過光の場合 |
M=τE〔lm/m2又はrlx〕 |
τ:透過率 |
E:照度〔lx〕 |
|
|