|
REAL TIME PREDICTION OF PHYTOPLANKTON BLOOM
In this study, we have fixed one hidden layer and 15 nodes of hidden layer under same calculation condition for case study in order to find optimized real-time prediction of environmental factors.
To avoid over fitting, we took account of the stopping point of the training. In ANN, the stopping point of training must be fixed, i.e., the number of iterations calculated by the system. We calculated the mean sum of errors (MSE). At each iteration, the learning system modifies the weights to minimize because the MSE decreases after learning. At the end of some thousand of iterations, the MSE is practically nil. The result stabilized after 50,000 iterations in our computation. We used the internal network parameters include the learning rate (μ =0.2), momentum (α =0.8) and transfer function (a =3). The initial weights were randomly distributed between 0 and 1.
The water temperature, salinity, dissolved oxygen and meteorological data (solar radiation, precipitation, air temperature) at the Observation Tower are available for data set and two species of phytoplankton, diatom and dinoflagellate are used for output. In this study, we do not consider the effect of nutrient concentration, because a real-time measurement of these values is very difficult.
Before this experiment, we calculated the correlation between various environmental factors, as like wind, humidity et al., and phytoplankton, and choose high correlation values among these factors for prediction of phytoplankton using neural network.
In order to find the optimum limited data set, and to investigate the effect of using different data for training and predicting on the generalization ability, the neural network were trained using input and output data set (Table 1) of 1999, and 2000, and then predicted phytoplankton bloom only using input data set of 2001 . Case 1〜5 do not considered of east current trend, but case 6〜10 do consider it.
Table l. Decision of inputs and correlation coefficients between predicted
and observed values.
| |
Input data |
Dinoflagellate(R2) |
Diatom (R2) |
| Case 1 |
Water temp, Salinity, A.T., SR, Precipitation, D.O. |
0.734 |
0.636 |
| Case 2 |
Water temp, Salinity, A.T., SR Precipitation |
0.827 |
0.597 |
| Case 3 |
Water temp, Salinity, A.T., Precipitation |
0.453 |
0.362 |
| Case 4 |
Water temp, Salinity, SR, Precipitation |
0.578 |
0.353 |
| Case 5 |
Water temp, Salinity, A.T,, SR |
0.619 |
0.255 |
| Case 6 |
Water temp, Salinity, A.T,, SR, Precipitation, D.O., current |
0.867 |
0.785 |
| Case 7 |
Water temp, Salinity, A.T., SR, Precipitation, current |
0.789 |
0.623 |
| Case 8 |
Water temp, Salinity, A.T., Precipitation, current |
0.897 |
0.390 |
| Case 9 |
Water temp, Salinity, SR, Precipitation, current |
0.451 |
0.534 |
| Case 10 |
Water temp, Salinity, A.T., SR, flow |
0.738 |
0.390 |
|
Table 1 and Figure 6 show the comparison of prediction and observation. The correlation coefficients of case 1 and case 2 are high for phytoplankton prediction. However these cases do not predict the peak point of observed phytoplankton concentration. To improve this weakness, we added current data as input data set (case 6 and case 7) resolution in more high correlation coefficients and predicting the peak period trend. As Figures 3 and 4, the current information, which has a period character and its transferring, should affect the ANN prediction of biological distribution. The high precision case for the prediction of dinoflagellate is case 8, which is also improved prediction accuracy by including the current whereas the prediction of diatom is not significantly improved.
Among the predicted results of cases, we divided the adaptable prediction system into two-group cases 1, 2, 6, 7 and the others. These results show it is able to predict real-time variation of phytoplankton with temperature, salinity, solar radiation, air temperature, and precipitation, and improve the prediction value adding currents.
To determine the relative significance of each input on the output, the following indicators is defined as a relative important parameter:
Figure 7 shows that the relative importance of the various input factors can be shown by examining these connection weights. These results indicate that the most important significant factors are changed according to input factors, and the neural network accuracy improved as more input variable are provided
| (Enlarge: 53KB) |
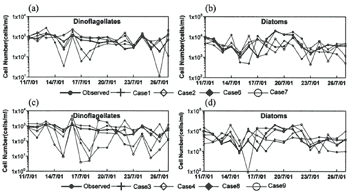 |
Figure 6. Comparison of each case (1, 2, 6, 7, 3, 48, 9) predicted and observed
results
| (Enlarge: 33KB) |
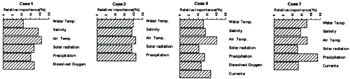 |
Figure 7. Relative importance between input and output of case 1,26 and
7
CONCLUSIONS
This study demonstrated that a generic ANN phytoplankton model structure in terms of inputs and outputs could be applied with different conditions in terms of water quality, climate, database characteristics, and achieve reasonable predictive accuracy. The ANNs model structured to forecast phytoplankton abundance proved to be successful for most, but not all, case studies investigated in this work.
Real-time prediction of the variation of phytoplankton species was conducted by using the observation data in Tanabe Bay and the artificial neural network (ANN) in this study. We changed the input data of ANN for finding the optimum, limited input data which is necessary for a real time estimate. It is found that ANNs is able to predict real-time variation of phytoplankton with temperature, salinity, solar radiation, air temperature, and precipitation, without nutrients and current information improve the prediction accuracy.
REFERENCES
Abdi, H. 1994. A neural network primer. Journal of Biological Systems. 2(3),247-283.
Fasham, M.J.R., H.W. Ducklow and S.M. McKelvie. 1990. A nitrogen-based model of phytoplankton dynamics in the oceanic mixed layer. Journal of Marine Research. 48:591-639.
Moloney, C.L. and J.G. Field. 1991. The size-based dynamics of plankton food webs. I. A simulation model of carbon and nitrogen flow. Journal of Plankton Research. 13:1003-1038.
Rumelhart. D.E., G.E. Hilton and R.J. Williams. 1986. Learning representations by back-propagating Errors. Nature 323.533-536
Steele, J. 1974. Spatial heterogeneity and population stability. Nature. 248,83.
Yoshioka, H. et.al 1998. The water exchange of Tanabe Bay in summer induced by internal kyucho. Proceedings of Coastal Engineering. JSCE, 45, 456-460.
|