|
ANALYSIS OF DISSOLVED OXYGEN AND TRANSPORT OF FISH EGGS IN A BAY
Yoshihiro Suenaga1, Koichi Masuda2, Takashi Sasaki1, Hee-Do Ahn3, Tetsuro Kobayashi1, Takashi Hoshino4 and Kaori Yasuoka4
1Faculty of Engineering, Kagawa University
Takamatsu, Kagawa Pref., JAPAN
suenaga@eng.kagawa-u.ac.jp
2College of Science and Technology, Nihon University
Chiba, JAPAN
3Korea Ocean Research and Development Institute
Seoul, KOREA
4Kuroshio Marine Technology, Co, LTD
JAPAN
ABSTRACT
Coastal aquaculture has been increased and developed in a semi-enclosed bay. In Seto inland Sea, Japan could produce marine aquaculture productions to supply the population demands. While the feeding rate of fish farming in Sido Bay, Kagawa Pref., Japan is approximately 12,378 tons a year, with the highest rate in summer. Therefore, the pollution from floating aquaculture cage can affect the environment via fecal waste, dissolved waste and excess feed settles. After the field experiments, it was found the tidal current, bottom topography and DO consumption rate by sediment are important factors to evaluate the canying capacity of aquaculture grounds. The authors proposed a more appropriate evaluation method for DO by using three-dimensional numerical model taking the effect of oxygen consumption by the fish in the aquaculture cage and bottom sediment into consideration. In this study has revealed that transportation of fish eggs and larvae from spawning ground to the nursery ground in and around the semi-enclosed bay by using numerical simulation model. Then, it is necessary to take the system for creating fishery ground and to estimate the carrying capacity of aquaculture grounds.
INTRODUCTION
Sido Bay is a small coastal aquaculture system that located 34°20'N and 134°11'E.
The climate in this region is influence by the tidal current, the Seto Inland Sea Japan. The bay is about
6 km in length and approximately 4 km in width at the mouth with a surface area of ca. 20 km 2
average depth of 8.3 m and the total water volume of ca. 140 m 3 (Fig.1). Recently
variable environmental problems have been caused by red tide, such as poor oxygen concentration at the
bottom, exploitation of sand resources for construction materials and many kinds of coastal developments.
Although aquaculture habitats in the Sido bay have been decreased, the impact of aquaculture on environment
could be manifest in a wide variety of ways (i.e. waste feed setting and oxygen deplete). We have conducted
field research to confirm the oxygen consumption by the fish in the aquaculture cage and bottom sediment
by using undisturbed core method. In this paper, we described a more appropriate evaluation method for
the carrying capacity of aquaculture grounds by using three-dimensional numerical simulation models ( Suenaga
et al., 1996; Fujihara et al., 1997) taking the effect of oxygen consumption
rate at each area in Sido bay into consideration. Also, the authors calculated the transport of fish eggs
and larvae in and around the Bisan-Seto area to clarify the nursery ground by using Euler-Lagrangian method.
This method is useful in estimating the carrying capacity for aquaculture grounds in a semi-enclosed bay.
| (Enlarge: 64KB) |
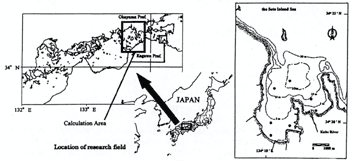 |
Figure 1. Bottom topography of Sido bay
●Collection of water and sediment samples
MATERIALS & METHODS
Governing equations
The current in the Sido bay is under the influence of tidal current and west
and east component of current is predominant along the both shores of Okayama Prefecture and Kagawa Prefecture.
A multi-level model ( Suenaga et al., 1996; Fujihara
et al., 1997; Suenaga et al., 1999; Sakuta et al., 1993) presently employed
is represented by the momentum equation on the rotating earth accepting f-plane and hydrostatic approximations,
the continuity equation, equation of free surface, the diffusion equations of water temperature and salinity
and DO and state equation, as follows (Eqs. (1)-(8));
| (Enlarge: 5KB) |
 |
| (Enlarge: 11KB) |
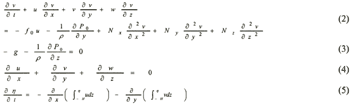 |
For T
| (Enlarge: 6KB) |
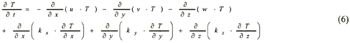 |
For S and DO
| (Enlarge: 8KB) |
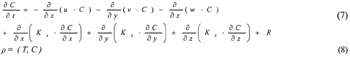 |
where u and v are the horizontal current vectors, w the
vertical current velocity, T the water temperature, C is the state variables (the salinity,
S and DO), ρ the density of water, g the acceleration due to gravity, f (=8.15 ×
10-5 /s: at 34°N) the Coliolis parameter, η the elevation from the mean
sea level (positive upward), H the water depth, Nx, Ny
(=0.01 m2/s) and Nz {friction coefficient at
surface (=0.0013): bottom (=0.0026): internal (=0.0001)} the horizontal and vertical eddy viscosity coefficients,
kx (=104cm/s) and ky
(=1 cm2/s) the horizontal and vertical turbulent diffusion coefficients of water
temperature, Kx , Ky (=104
cm2/s) and Kz (= 1 cm2/s)
the horizontal and vertical diffusion coefficients of salinity and k the unit vector(positive upward),
respectively (Sasaki and Inoue, 1984).
In the diffusion equation of DO, the last term "R" in equation (7) includes the DO flux by water surface (Sasaki and Inoue, 1984). Re-aeration, consumption rate (A:0.003, B:0.004. C:0.005, D:0.008, ml/sec/m2) by the respiration of fish (yellowtail fish), consumption by suspended matters (0.068ml/l/hr) and sediment. Also, the consumption rate by sediment (A:0.017, B:0.017, C:0.018, D:0.018, ml/sec/m2) was measured by undisturbed core method.
Euler-Lagrangian Method
The eggs and larvae treated as particles were traced in the computed flow field for their planktonic period (27 days) using the Euler-Lagrangian Method. The governing equations are as follows:
| dX/dt=V (9) |
| X(0)=X0 (10) |
| X(n+1)*=X(n)+F(n)Δt (11) |
| X(n+1)=X(n)+(F(n)+F(n+1)*)/2*Δt (12) |
| F(n)=V(n)+{(V(n)・∇)V(n)}Δt (13) |
where X is the position, V the velocity, ∇ the horizontal differential
operation, Δt (=20s) the time increment; superscript means the time level and * is temporary value at
the time level. Initial value problem of the differential equations expressed in equations (9) and (10)
is solved using two-step Runge-Kutta integration method expressed in equations (11)-(13). The velocity
and shear at the egg/larva position are calculated by interpolation using surrounding values. Particles
are located the depth of 10 m and transported only by water movement for the first 3 days and then gradually
swim up to the depth of 3 m for 12 hours ( Nakata et. al., 1999). After that
they gradually swim down to depth of 10 m for 12 hours, and they repeat that movement during 27 days.
Computed domain
Figure 2 shows the computed domain of this study area. The bottom topography in and around the Western Bisan-Seto area and computational domain are shown in Figure 2. The whole body of water is described into 500 m × 500 m square meshes horizontally and three levels vertically (1st level:0-6m, 2nd level:6-15 m, 3rd level:15 m-bottom) for the computation. Tidal flow (tidal level: half amplitude=1 m) is given at the each entrance of Bisan-Seto area as a boundary condition. The flow fields were first reproduced using a multi-level density flow model with observed velocities as boundary tidal conditions. In Sido Bay, the whole body of water is described into 100 m × 100 m square meshes horizontally and six levels vertically (1st:O-1.5 m, 2nd:1.5-3.5 m, 3rd:3.5-6.5 m, 4th:6.5-9.5 m, 5th:9.5-25.5 m, 6th:25.5 m-bottom) for the computation. Tidal flow is given at the each entrance of Sido bay as boundary conditions shown in Table 1. Also, river discharge was added from Kabe-river (3.9 × 104 m3/day) to the sea (Fig.1).
Table 1. The boundary conditions for calculation
| Area |
Amplitude (m) |
Period (hr) |
Phase lag (deg) |
| A |
0.563 |
12.42 |
324.5 |
| A' |
0.563 |
12.42 |
324.5 |
| B |
0.456 |
12.42 |
331.9 |
| B' |
0.456 |
12.42 |
331.9 |
|
| (Enlarge: 71KB) |
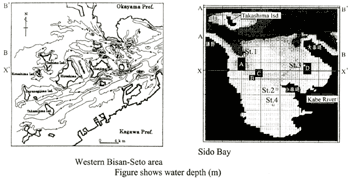 |
Figure 2. Computed domain of each study fields
|