|
FLOW PARAMETERS BEHAVIOR DURING WAVE RUN-UP AND DRAWN-DOWN
Proposed method makes it possible to calculate and watch all flow parameters during whole process (tsunami wave run-up and drawn down). For example the flow velocity is one of the most important parameters of the wave during inundation process. It determines the force of the wave impact to the shore structures. Potential force of the flow per unit shore width is proportional to the water layer thickness and the squared flow velocity (η+H)・V2. In Table 4 the values of flow parameters, which are written in the second column, are given for almost all coastal grid-points. Their numbers are given in the first row of this table. In the first column the initial tsunami wave period (parameter b in formula (3)) and amplitude (η0) are given. In these computations the shore slope was constant and equal to 0.1 (tg α). After the analysis of flow parameters, given in Table 4, we may conclude that during the wave run-up the maximum flow velocity is registered in grid-points which are located at a quarter of the final run-up length from the initial water edge point. For instance the maximum of the water flow rate during the 6 m high wave run-up is detected in the 6th grid-point of the total 20 inundated grid-points. In the same numerical experiment the flow velocity during the wave drawn-down was much greater in all coastal grid-points with maximum of 24 m/sec near the initial water edge point. The integrated parameters η・V and η・V2 reach their maximums near the initial water-edge point because of big water-layer thickness during inundation process in these points.
MODELING OF TSUNAMI RUN-UP ON A REAL SHORE
Numerical modeling of the long wave run-up on the real shore was carried out. The profile of the Japan coast (Fig.6) was taken from Survey Report of Tsunami of May 26 1983 Along the Coasts of Akita Prefecture (Akita Prefecture Office Report, 1984). In this place (near Minehama village) run-up height was recorded as 14.08 m. To reach such a height the incident tsunami wave with the period 65 sec must be about 8 meters high near the coastline. The wave profile in this case is shown in the Figures 7-8.
CONCLUSIONS
The new algorithm of tsunami wave run-up computation a on a shore of an arbitrary profile is developed. The results of the wave run-up on a sloping shore are in good agreement with the results obtained earlier with the help of analytical and numerical methods. The computational experiments of a tsunami impact on a shore of an arbitrary profile have revealed such type of shore relief, which gives the highest climb of the water on the shores of various profiles with identical initial wave. The destructive tsunami effect due to the water-flow force is bigger when the affected structure is closer to the initial water edge. The wash-away force is much greater than water flow force during run-up. The described model reasonably simulates tsunami wave run-up on a beach with arbitrary profile and can be used in simulation of real tsunami waves. Two-dimensional description of the flow near the moving water edge point is the main advantage of this method
Table 4. Flow parameters during tsunami wave run-up and drawn-down
| Wave parameters |
Measured value |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
| b=0.05 η0=4 |
Vmax |
4.67 |
4.50 |
4.26 |
3.93 |
3.60 |
3.44 |
3.02 |
2.80 |
2.25 |
1.79 |
1.54 |
0.09 |
|
|
|
|
|
|
| |
Vmin |
-15.3 |
-13.9 |
-13.1 |
-12.0 |
-11.2 |
-10.1 |
-9.23 |
-8.15 |
-6.97 |
-5.54 |
-3.66 |
-0.52 |
|
|
|
|
|
|
| b=0.05 η0=5 |
Vmax |
4.69 |
4.71 |
4.80 |
4.77 |
4.69 |
4.60 |
4.48 |
4.38 |
4.22 |
4.00 |
3.76 |
3.43 |
2.95 |
2.23 |
1.35 |
|
|
|
| |
Vmin |
-16.4 |
-15.5 |
-14.9 |
-13.9 |
-13.3 |
-12.4 |
-11.8 |
-10.9 |
-10.1 |
-9.21 |
-8.24 |
-7.14 |
-5.90 |
-4.36 |
-1.95 |
|
|
|
| b=0.05 η0=6 |
Vmax |
4.80 |
5.04 |
5.45 |
5.63 |
5.72 |
5.76 |
5.74 |
5.73 |
5.66 |
5.52 |
5.31 |
5.19 |
4.96 |
4.63 |
4.26 |
3.73 |
3.12 |
2.30 |
| |
Vmin |
-24.3 |
-22.3 |
-20.0 |
-19.0 |
-17.7 |
-16.5 |
-15.6 |
-14.5 |
-13.7 |
-12.8 |
-12.0 |
-11.1 |
-10.2 |
-9.31 |
-8.28 |
-7.25 |
-5.81 |
-4.13 |
| b=0.03 η0=5 |
Vmax |
2.11 |
2.09 |
2.62 |
2.71 |
2.54 |
2.20 |
2.17 |
2.06 |
1.53 |
1.32 |
1.04 |
0.25 |
|
|
|
|
|
|
| |
Vmin |
-14.9 |
-13.9 |
-13.2 |
-12.4 |
-11.4 |
-10.4 |
-9.31 |
-8.21 |
-6.99 |
-5.61 |
-3.84 |
-1.05 |
|
|
|
|
|
|
| b=0.05 η0=5 |
(η×V)max |
31.8 |
28.9 |
26.1 |
23.1 |
20.6 |
17.9 |
15.2 |
12.9 |
10.2 |
8.12 |
6.15 |
4.40 |
2.91 |
1.56 |
0.47 |
|
|
|
| |
(η×V)min |
-47.1 |
-42.3 |
-38.6 |
-34.3 |
-30.6 |
-26.8 |
-23.2 |
-19.8 |
- 16.4 |
-13.2 |
-10.2 |
-7.31 |
-4.63 |
-2.28 |
-0.43 |
|
|
|
| |
η×(Vmax)2 |
144 |
127 |
115 |
101 |
88 |
76.8 |
63.4 |
52.0 |
41.8 |
31.6 |
24.5 |
17.5 |
11.6 |
6.8 |
3.0 |
0.5 |
|
|
| |
η×(Vmin)2 |
603 |
543 |
461 |
407 |
341 |
292 |
240 |
197 |
156 |
120 |
88.0 |
60.9 |
37.5 |
19.5 |
7.0 |
|
|
|
| b=0.05 η0=6 |
(η×V)max |
45.4 |
43.7 |
38.9 |
36.1 |
33.3 |
30.0 |
26.7 |
23.4 |
21.4 |
17.8 |
15.2 |
12.7 |
10.4 |
8.07 |
6.01 |
4.16 |
2.58 |
1.17 |
| |
(η×V)min |
-60.2 |
-55.7 |
-51.7 |
-47.3 |
-43.6 |
-39.3 |
-35.7 |
-31.9 |
-28.2 |
-24.9 |
-21.3 |
18.2 |
-14.9 |
-12.0 |
-9.07 |
-6.39 |
-3.89 |
-1.73 |
| |
η×(Vmax)2 |
245 |
227 |
215 |
184 |
183 |
160 |
139 |
122 |
107 |
93.9 |
72.6 |
63.2 |
50.6 |
39.1 |
27.8 |
19.3 |
12.0 |
6.4 |
| |
η×(Vmin)2 |
877 |
788 |
702 |
627 |
552 |
490 |
423 |
371 |
314 |
267 |
221 |
179 |
144 |
108 |
80.0 |
53.5 |
32.7 |
16.1 |
|
| (Enlarge: 12KB) |
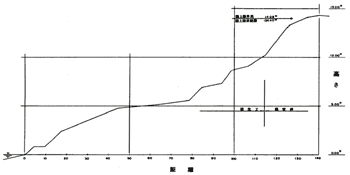 |
Figure 6. Shore profile near Minehama village in Akita prefecture (Japan)
Figure 7. Modeling of Japan Sea Tsunami 26.05.1983 at the Akita coast. Tsunami
wave profiles at the moment of highest run-up
REFERENCES
Akita Prefecture Office Report. 1984. Survey Report of Tsunami of May 26 1983 Along the Coasts of Akita Prefecture (in Japanese) Japan: Akita Prefecture Office.
Marchuk An. G. 1982. Method for computations of long gravity waves run-up on sloping shore (in Russian). Tsunami evolution from the source up to run-up on a shore Moscow: Radio i Sviaz.
Pelinovsky E.N. 1982. Nonlinear dynamics of tsunami waves (in Russian) Gorky: Institute of Applied Physics RAS.
Pelinovsky E.N. 1985. Tsunami Run-up on a shore (in Russian) Gorky: Institute of Applied Physics RAS.
|