|
THE FLOW PARAMETERS ESTIMATION ABOVE DRY LAND IN THE TSUNAMI RUN-UP MODELING
Andrey G. Marchuk and Alexandr A. Anisimov
Institute of Computational Mathematics and Mathematical Geophysics Siberian Division of the Russian Academy of Sciences, Novosibirsk, RUSSIA
mag@omag.sscc.ru
ABSTRACT
The most important question in the prognostic tsunami modeling is estimation of tsunami run-up heights at different points along the coastline. Also, it is of great importance to know the water flow velocity in submerging areas, because a high-speed flow during tsunami run-up is the main destructive factor of a tsunami attack. In the paper the new method for numerical simulation of the long wave run-up process is proposed. Nonlinear shallow water equations are used for description of the wave propagation up to the water-edge point. Then the special algorithm used for estimation of the flow parameters and location of the moving water edge. It is based on the energy and mass conservation laws. Several series of one-dimensional computations were carried out. Shore profile, which gives the maximum run-up height for the fixed initial wave parameters have been found. Results of modeling of the tsunami run-up on the real shore in the Akita prefecture (Japan) are presented.
INTRODUCTION
One of the most important questions in prognostic tsunami modeling is estimation of tsunami run-up heights in different points along the coastline. Methods for numerical simulation of tsunami waves propagation in deep and shallow sea are well developed and are widely used by a great number of scientists. Some of them, in order to find possible submerged areas use the simplifying assumptions about the ratio between the tsunami wave height near the shore and wave's run-up height. But this ratio strongly depends on the shore profile above mean sea level.
STATEMENT OF THE PROBLEM
In this paper the method for numerical calculation of tsunami waves run-up on a shore of arbitrary profile will be described. Numerical modeling of this process was carried out based on the one-dimensional nonlinear shallow-water model
| ut+uux+gηx=0, |
| ηt+(u(η+H ))x=0, (1) |
where u - velocity, η - surface elevation, H - the value of depth. The problem statement is as follows: there is one-dimensional nearcostal area with an arbitrary bottom relief. From the left boundary of computational area tsunami wave is coming toward the shore. Above the mean sea level the coast have arbitrary profile (Fig.1).
Figure 1. The statement of the run-up problem
The shore surface above the mean sea level has an arbitrary profile. In numerical computations it is given as an array of elevation values in grid-points. Bottom relief can have any form. In the beginning, the water in the area is still, so the initial conditions can be written as
u(x,0)=η(x,0)=0 . (2)
The incident tsunami wave is generated by water motion and moving of a free surface on the left boundary of computational area
After the wave is formed completely (it will happen, when the time value t will become equal to 2π/b), the "free" boundary conditions will be assigned to this boundary
NUMERICAL ALGORITHM
The differential problem (1)-(4) is solved numerically with the help of method of finite differences. So all the variables are defined in the grid-points and the values of the depth and topography elevation is given as the array Hi (i=1, M). The explicit finite difference equations with central differences
| (Enlarge: 8KB) |
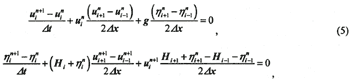 |
are used for computations in the inner points of the area. Values of the velocity
uin+1(i=1,M) are preliminary defined from the first
equation (5) in whole computational area. Then from the second equation (5) one can define the values
of the surface elevation ηin+1on the higher time level in all inner grid-points.
On the right boundary (the coast) where the depth value is equal to zero or is very close to this value (〜0.01m) the "free" boundary conditions (4) are used until the moment, when the surface disturbance will reach this boundary grid-point. From this moment the special algorithm for computation of the flow parameters is used.
Let introduce the new computation point B, which shows the location of the water-edge point in every discrete time moment (time step). The position of this point is determined by calculating the volume of water, which comes through the cross-section MC during every time interval (Fig.2). We assume that the surface profile between points A and B represents a straight segment. The location of the point B can be calculated from the total water volume rightwards the cross-section MC.
Figure 2. Definition of the water edge-point location
The distance between a projection of a point A and projection of a water edge point B cannot exceed one computational step on space. The change of a volume at each step is summarized and based on the full volume (square of a triangle MCD) the new position of a point of a water edge is determined. The scheme of the given algorithm is drawn in Figure 2.
Let at some time moment the points E and A show positions of
the free surface at computational grid-points with numbers M-1 and M accordingly and point B -
position of the point of a water edge at this moment. Elevation of the free surface and water velocity
in the grid-point M-1 are calculated by difference scheme (2). And in the grid-point M this can be done
using the following procedure: at first we define new values of velocity and elevation ( 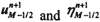 )
in a midpoint between grid-points with numbers M-1 and M using difference equations
| (Enlarge: 9KB) |
 |
And in a midpoint between points M and B (values 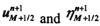 ):
| (Enlarge: 9KB) |
 |
Then with the help of a linear interpolation values of velocity and elevation on the new time level are define in the grid-point with number M.
| (Enlarge: 8KB) |
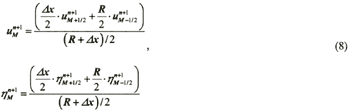 |
Here the value R represents distance along the horizontal axis from the most right computational grid-point up to a current position of the water edge point, and the gridded variables with index M+1- are values of flow parameters in the mobile point of a water edge. The water-edge velocity is determined from the mass and energy conservation laws.
| (Enlarge: 5KB) |
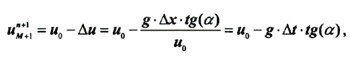 |
where u0 is the preliminary water edge velocity, estimated from the one time-step increment of the triangle MAB square value (Fig.2) and tg(α) is the shore inclination between M and M+1 grid-points. If the distance between projections of points C and D becomes greater than step of spatial computational grid then we introduce the new grid-point with number M+1 and the computational algorithm moves to this new grid-point.
|