|
ANALYSIS AND RESULTS
Table 1. The parameters assumed for simulation
| Vessel speed |
5 m/s (approx. 10knots) |
| Roll, pitch and heave period |
10 s |
| Roll, pitch peak-to-peak amplitude |
20° |
| Heave peak-to-peak amplitude |
2m |
| Echosounder frequency |
38 kHz |
| -3 dB full beamwidth |
7° |
| Ping period |
1 s |
|
In this section, simulation results for TRF, TSE and EL will be presented. The appearance of target traces and echo intensity is controlled by such factors as transducer beam pattern, relative speed between vessel and target, vessel motions and target range. Sinusoidal vessel roll, pitch, yaw and heave functions will be used to illustrate these effects. The parameters assumed to illustrate these effects are given in Table 1.
Effects of Vessel Motion on TRF and TSE
The TRF (Target Range Function) and TSE (Target Strength Error) for a stationary target observed from a vessel moving in calm seas are shown in Figure 3. TRF has an "inverted V" shape because the minimum target range will occur for the smallest horizontal distance between target and vessel. TSE is zero dB when the target is on the acoustic axis, which occurs at zero horizontal vessel to target distance. TSE increases with increasing distance from the center or, equivalently, with increasing angle from the acoustic axis. The transducer and target locations are A11(0,0,0) and P11(0,0,100), respectively. This implies that the transducer passes directly over the target at zero distance. TRF and TSE are continuous functions. The dots on the TRF and TSE diagrams represent the samples of these functions obtained by the acoustic pings. The pinging frequency may not be sufficient to reconstruct these functions (as postulated by the Nyquist sampling theorem). Actual echograms use a threshold that is set to eliminate ambient and other noise. For the sake of exposition we have assumed zero threshold and zero noise condition.
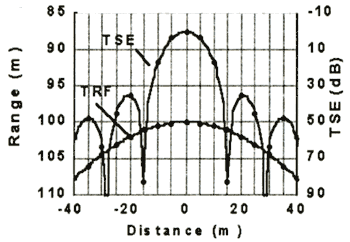 Figure 3. TRF and TSE for a stationary target observed from a moving vessel
with no roll, pitch, yaw or heave. The x-axis represents distance travelled by the vessel with respect
to target position.
More irregular patterns are observed when vessel roll and pitch are introduced, as shown in Figure 4. A sine function that is zero at zero distance simulates roll and pitch. The asymmetry in the sine function is reflected in the asymmetry in TRF and TSE. Additional asymmetry is added by locating the transducer at A11 (4,0,2), a position which is no longer at the centre of the rotation.
Figure 4. TRF and TSE for a stationary point target observed from a moving
vessel (a) with vessel roll only, (b) with vessel pitch only.
Larger irregularities are seen in Figure 4b than in Figure 4a as pitch effects will add to or subtract from the vessel's forward motion while roll effects are perpendicular to that motion. Although not shown, yaw rotation will have relatively little effect on TRF and TSE, because yaw rotation is about the z-axis and is at least approximately aligned with the symmetric beam pattern of the circular piston transducer used here.
Figure 5. (a) TRF and TSE from a stationary point target (a) with vessel
heave, (b) with vessel roll, pitch, yaw and heave.
Figure 5(a) shows the effect of vessel heave. Both TRF and TSE are similar to those in Figure 3 but heave effects are clearly stronger on TRF than TSE since heave adds to target range and has relatively little effect on the off axis target angle. The TRF and TSE functions shown in Figure 5(b) include roll, pitch, yaw and heave effects. Among the four motions, the effect of roll and pitch rotations are significant in TSE and heave plays an important role in TRF. Figures 4 and 5 use the same asymmetric transducer location. The resulting shift in TRF and TSE relative to distance is apparent in both figures.
TRF and EL Based on Real Vessel Motion Data
Figure 6. Typical 150-second time series of roll, pitch, yaw and heave from
Miller Freeman motion history.
In this section, we will demonstrate the effects of measured vessel motion data on TRF and EL. Figure 6 shows a brief sample from the motion that was experienced by the NOAA research vessel Miller Freeman 2-3 March 2001. Target traces based on real vessel motion data and sonar parameters as given in Table 1 are synthesized and presented in Figure 7. The figure shows the relative echo level from seven simulated targets at 10 and 2-knot vessel speed. The traces were terminated for EL below -90dB.
Figure 7. Seven target tracks based on measured vessel motion data and synthetic
target information. (a) Vessel speed 10 knots (b) Vessel speed 2 knots
COMPENSATION FOR VESSEL MOTION EFFECTS
Our work suggests two new options to compensate and minimise the adverse effects of vessel motion on the acoustic detection of single fish targets:
1. An inverse form of our simulation model can be used to correct acoustically measured target positions; and
2. Echosounder transmissions may be synchronised with vessel motion.
Both methods require that vessel motion measurements are available. The former method also requires target position information that may be obtained from split-beam measurements. Given accurate vessel motion measurements the model and rotation matrices used for our simulation could, for example, be applied to vessel based, split-beam target position measurements to obtain estimates of target position and movement in a fixed reference frame. This information is essential for fish tracking and fish flux measurements that provide new insights into fish behaviour and migration. Fixed, split-beam installations, now used in many rivers, provide this kind of information (Enzenhofer et al., 1998). The second approach only depends on the availability of real-time vessel motion measurements that can be used to trigger echosounder transmissions at specific times rather than at constant time intervals. An obvious time for synchronised transmissions occurs when the vessel is in a near level position. Difficulties are that near levelled positions may occur too infrequently and that the rate of change for angular position will tend to be largest at that time. The method may, however, be useful in specialised situations.
Alternate methods for minimising the adverse effects of vessel motion include the use of a hull mounted and stabilised transducer or of a towed body that travels behind the vessel. Our model and simulation will be useful to explore the effectiveness and feasibility of these and other procedures designed to improve acoustic observations from a moving platform.
CONCLUSIONS
This paper presents a model and simulation results that demonstrate the adverse effects of vessel motion on single target detection and on the echogram. These effects are illustrated in a series of figures based on synthetic and real vessel motion data.
We come to the following conclusions:
1) In fisheries acoustics, measurements, such as echo integration, echo counting and TS measurement, are affected and degraded to an often-unknown degree by vessel motion.
2) For a vertically aimed transducer, the secondary vessel motions have different effects on TRFs and TSEs. Yaw by itself has little effect, while roll, pitch and heave might cause significant distortion. Superposition of all four motions can cause significant distortions on both TRF and TSE.
3) Analytical compensation is possible when secondary vessel motions are measured. Compensation will be limited when vessel motions are large enough that targets are prematurely lost from the beam.
4) Additional methods transducer stabilisation, variable ping rate and beaming steering should be considered, as the potential for correction appears to be limited.
5) Our model and simulations can provide an effective tool to assess the adverse effects of vessel motion and the effectiveness of actual and proposed compensation procedures. And it can provide a warning when a specified level of vessel motion and hence echogram distortion is exceeded.
ACKNOWLEDGEMENT
The Miller Freeman vessel motion data used in Figure 7 was kindly provided by N. J. Williamson from the National Marine and Fisheries Service, Seattle, Washington. This work was partially supported by a grant from Natural Sciences and Engineering Research Council of Canada. Authors are appreciative to anonymous reviewers for their constructive comments.
REFERENCES
Clay, C.S., and Medwin, H. 1977 Acoustical oceanography: principles and applications. John Wiley & Sons. New York.
Cushing, D.H. 1973. The detection of fish. Pergamon Press, Oxford.
Dunford, A.J. 2002. Correcting acoustic data for transducer motion. ICES Symposium on Acoustics in Fisheries and Aquatic Ecology, Montpellier, France, June 10-14, 2002. Paper # 68.
Enzenhofer, H.J., Olsen, N., and Mulligan, T.J. 1998. Fixed-location riverine hydroacoustics as a method of enumerating migrating adult Pacific salmon: Comparison of split-beam acoustics versus visual counting. Aquatic Living Resources, 11(2):61-74.
Furusawa, M. and Sawada, K., 1991. Effect of transducer motion error on quantifying single fish echoes. Nippon Suisan Gakkaishi. 57:857-864.
Hare, R., Godin, A., and Mayer, L. 1995. Accuracy estimation of Canadian Swath (multibeam) and Sweep (multi-transducer) sounding systems. Canadian Hydrographic Service, Sydney, BC.
Harrington, S. 1987. Computer graphics: A programming approach. McGraw-Hill, New York.
Hearn, D., and Baker, M.P. 1986. Computer graphics. Prentice-Hall, New York.
Maclennan, D.N., and Simmonds, E.J. 1992. Fisheries acoustics. Chapman & Hall.
Stanton, T.K. 1982. Effects of transducer motion on echo-integration techniques. J. Acoust. Soc. Am., 72(3):947-949.
Stephens, R.W.B. 1970. Underwater Acoustics. John Wiley & Sons Ltd.
Traynor, J.J. and Ehrenberg, J.E. 1990. Fish and standard-sphere target-strength measurements obtained with a dual-beam and split-beam echo-sounding system. Rapp. P.-v. Reun. Cons. int. Explor. Mer, 89:325-335.
|