|
RESULTS AND DISCUSSIONS
Verification of prediction methods
The calculation results of distributions of vertical displacement on y=0 are compared in order to verify the validity of the prediction methods in Figures 4 to 8. In the three-dimensional method, αequals 1.0. The height in order to calculate the volume of an aircushion is 5.0 meters.
In all of the figures, deformation characteristics of each model are agreement qualitatively although the both results have slight differences.
Figure 4. Comparison between deflection amplitudes of Model-0 calculated by present method and 3-D method on y=0.0
Figure 5. Comparison between deflection amplitudes of Model-1 calculated by present method and 3-D method on y=0.0
Figure 6. Comparison between deflection amplitudes of Model-2 calculated by present method and 3-D method on y=0.0
Figure 7. Comparison between deflection amplitudes of Model-3 calculated by present method and 3-D method on y=0.0
Figure 8. Comparison between deflection amplitudes of Model-4 calculated by present method and 3-D method on y=0.0
Reduction of elastic deflection in head sea conditions
In Figure 9, the comparison of vertical displacement distributions by χ direction
on y=0.0 is shown in case of L/λ=3.24. Figure 10 shows the results in case of L/λ=12.98.
The wave angle is 0 degrees in both results. It can be seen that the motion responses of Model-0 which
whole bottom area is the one aircushion are very small in the both wavelength ranges. In Figure 9, the
elastic deflection becomes small when the inner aircushion area is wider. However, a characteristic of
the deflection of Figure 10 that is shorter waves is reverse as compared with that of Figure 9. The response
of Model-5 is smallest in Figure 10. From the deflection characteristic of Model-5 differs greatly from
that of Model-3 and Model-4, it is expected that width of outer aircushion to the wavelength influence
the elastic deflection greatly.
Figures 11 (a) and (b) show results of the distribution of vertical displacement of Model-1. Model-1 has little motion response in an oblique wave and a beam sea with relatively long waves. The examination on Model-1 is neglected in longer wave ranges because it is expected easily that the response became smaller.
Figure 9. Comparison of deflection amplitude in L/λ=3.24
Figure 10. Comparison of deflection amplitude in L/λ=12.98
| (Enlarge: 10KB) |
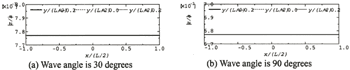 |
Figure 11. Deflection distributions of Model-1 in L/λ=4.67
Behaviors of wave field around floating structures
Counter maps of a wave height distribution around the calculation models are shown in Figure 12 where the results are normalized by height of an incident wave. The behavior of the wave field includes an influence of the elastic deflection of the floating structure. A counter at structure area means amplitude of the elastic deflection. The wavelength corresponds to L/λ=12.98. The range of the counter maps is from 0.0 to 2.0 other than that of Model-1. In the results of Model-1, the range of the counter maps is expanded since the incident wave is mostly transmitted. In blue colder areas, the wave height is over from maximum value of the counter range.
In the case of Model-1, most waves penetrate. Therefore, Model-1 supported by one aircushion at whole bottom area is an ideal floating type in order to reduce the elastic deflection and the wave drifting force simultaneously.
In the case where the wave angle is 0 degrees, the transmitted wave backward does not become large in Model-2. The transmission of the wave to behind of Model-5 does not become larger that of Model-0. However, the wave scattering is small to transverse directions. Therefore, it can be estimated to be able to reduce the wave drifting force.
It is necessary to narrow the width of the buoyant block or the bulkhead as much as possible in order to reduce the deflection and the wave drifting force. Then, it is thought that division of the aircushion does not become a demerit for the response reduction in order to secure the hydrostatic restoring force.
| (Enlarge: 121KB) |
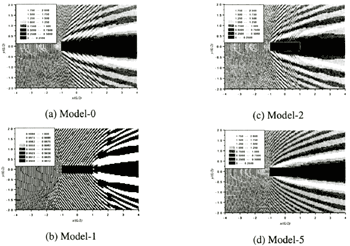 |
Figure 12. Counter maps of wave around floating structure in 0 deg. wave with L/λ=12.98
CONCLUSIONS
In this paper, two prediction methods for the analysis of the aircushion type VLFS are proposed. From the calculation results we conclude on the aircushion-supported elastic floating structure as follows:
1) The present zero-draft theory is useful for the prediction of the aircushion type VLFS.
2) Model-1 that is an ideal aircushion type is hardly moved in waves. Moreover, it is supposed to be able to reduce the wave drifting force from the results of the counter map of the wave behavior around the floating structure.
3) When the aircushion is divided to outer and inner aircushions, the width of the outer aircushion to a wavelength of an incident wave influences in the elastic deflection strongly. Moreover, the elastic deflection becomes small at mid-ship area when the buoyant block has the width that prevents the water wave into the inner aircushion. Then, the transmitted wave becomes small.
4) It is necessary to narrow the wall as much as possible in order to reduce the elastic deflection and the wave drifting force simultaneously.
ACKNOWLEDGMENTS
Part of this research was supported by Grant-in-Aid for Scientific Research from Japan Society for Promotion of Science.
REFERENCES
Ikoma, T., Masuda, K., Maeda, H., and Rheem, C.H.. 2002. "Hydroelastic Behavior
of Air-Supported Flexible Floating Structures," Proceedings of The 21st International Conference on
Offshore Mechanics and Arctic Engineering, OMAE'02 in Oslo Norway, ASME, OSU-28090,2002
Lee, C.H. and Newman, J.N., 2000. "Wave effects on large floating structures
with aircushions," Journal of Marine Structures, Vol.13, ELSEVIER SCIENCE, pp.315-330
Maeda, H., Masuda, K., Miyajima, S. and Ikoma, T., 1996. "Hydroelastic Responses
of Pontoon Type Very Large Floating Offshore Structure," Proceedings of The 15th International Conference
on Offshore Mechanics and Arctic Engineering (OMAE'96), ASME, Vol.I, pp.407-414
Maeda, H., Rheem, C.K., Washio, U., Osawa, H., Nagata, Y., Ikoma, T., Fujita,
N. and Arita, M. 2001. "Reduction Effects of Hydroelastic Responses on a Very Large Floating Structure
with Wave Energy Absorption Devices using OWC System," Proceedings of The 20th International Conference
on Offshore Mechanics and Arctic Engineering (OMAE'01), ASME, CD-ROM file OSU-5013
Pinkster, J.A., Fauze. A., Inoue, Y. and Tabeta, S. 1998. "The behaviour of
large aircushion supported structures in waves," Proceeding on Hydroelasticity '98 in Fukuoka Japan,
Edited by M. Kashiwagi, pp.497-506
Pinkster, J.A. and Meevers Scholte, E.J.A. 2001. "The behaviour of a large
air-supported MOB at sea " Journal of Marine Structures, Vol.14, ELSEVIER SCIENCE, pp.163-179.
|