|
EFFECT OF OCEANIC WATER LOADING
Using the model in Figure 1, vertical displacement
of the crustal surface (w) may be written as:
w=[S0H0] [2-exp(Gx) cos(Gx)] for x>0, (6)
and,
w=[S0H0] [exp(Gx) cos(Gx)] for x<0, (7)
where the initial crustal surface is assumed to be located on the line L-N in Figure 2, and the Z axis is taken to be upward positive.
Figure 2. Negative upheaval (solid line) as a combined function of a simple
harmonic function and exponential functions (dotted lines) referring to the reference sea level (L-N).
Denoting the densities of the crust as ρ and of the sea water as ρ0
, then,
G4= ρH/(4D), (8)
S0=ρ0/ρ, (9)
And, then, the distance between the crest to the next crest L' is written as follows:
L'= [(4/9)ρg] [E H^3], (10)
Where, G= 2π/L'.
If we denote S=2S 0 (referring to the line L-N in
Fig.2), then, it is easily understood that the crustal surface pattern can be illustrated by a solid line
of an undulation curve as shown in Figure 2. This pattern may be given as a product of exp (Gx) and cos
(Gx). Taking that S=0' at x=0, and using (4) and (5), then, the vertical displacement of the crustal surface
is shown by the solid line. The pattern of the solid line in Figure 2 is the final equilibrium state of
the crustal surface after the loading of the model ocean water as assumed in Figure
1. This might be similar to a corresponding geodetic isostasy (cf. Officer, 1974).
TROUGH AND RIDGE
In order to clarify what we are interested, the specific pattern of the solid
line is shown as a function w with a variable x (Fig.2). The value of w is the vertical displacement of
the crustal surface, and this can be taken as negative upheaval (Fig.3). The pattern of the negative upheaval
demonstrates the crustal surface near the coast (around the discontinuous place of the model ocean water
loading). The pattern of the negative upheaval relative to the sea surface may be, for example, as that
relative to the initial flat state L-N (Fig.2). This pattern shows that a significant negative upheaval
is seen by a loading to form a trough offshore and a minor positive upheaval is seen on landside after
loading to form a ridge. As for the location of the coastline, the initial coastline, assumed to be located
at the edge of the model ocean loading, is shifted horizontally to the side of the model land ( Fig.1).
What is noted above is the specific result caused by the loading of the model ocean on the model crust.
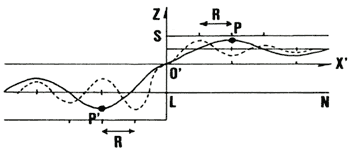 Figure 3. Negative upheaval for a given value of G=G0(solid
line) and that of G=2G0 (dotted line). Location of maximum (P) and minimum (P')
for G=G0 shifting as much as R relative to the origin of the coordinate (O')
with the reference sea level (L=N).
Formation of an offshore trough is caused by the loading effect of the static
ocean water on the elastic crust. As for the positive upheaval of the crustal surface, it can be seen
at a little distance on the land side of the crust, that is, on the side of x>0 in Figures 2 and 3.
This means that it is possible to find a mountain ridge just adjacent to the coastline after the loading
effect of ocean water. This shows also that the coastline moves to the landside of the model in Figure
1. If the thickness of the model ocean water is increased, then, amount of the upheaval is amplified
without any change of the shifted location of the coastline.
In Figure 3, it is shown what shifting of the trough and ridge can be expected when the value of G is twice of the value initially assumed in the above solution. The solid line is the same as that for the solution reduced first in this work, and the dotted line shows the solution for the value of 2G.
In this case, the location of the trough at x=P should shift to x=P-R, and, the location of the first maximum of the upheaval at x=P' should shift to x= P'+R (Fig.3).
When G=G0 at x=P and G=0 at x=0, the relationship between G0 and R for an arbitrary value of x' (in the range of 0<x'<P) is given (Fig.4). This shows that the slope between the trough and the ridge becomes steeper when the value of G becomes smaller. It should be noted That G4=ρH/(4D), and D=(1/12)[E^3] [1-σ^2]. Hence, the value of G is determined by the parameters ρ of and D, and the value of D is determined by the parameters E, H and σ. These parameters should be taken as the equivalent parameters for the model in this work.
Figure 4. Shift R from P for G=G0 at the same
phase of the simple harmonic function
Now, it might be helpful to introduce a nominal set of the equivalent parameters,
for convenience, for realizing what could be expected in the existing crustal upheaval pattern ( Nakamura,
2001).
Adding to the above, it is necessary to remind that the actual crust existing on the earth, has a very complicated geological structure in fact. Nevertheless, the model in this work is aimed for a macroscopic response of the crustal upheaval so that only a dynamical response of the model with a set of the equivalent elastic parameters. Although, the value of these parameters would not be same to the corresponding elastic constants of any one of the materials consisting the actual crust.
Officer (1974) provides some numerical case studies
that help us to understand what we see. For Lame's two constants, it is assumed that λ=μ=3.3x10^10Pa(=10x10^11
cgs), where the dimension of Pa corresponds to [N/m 2] (=10g/sec^2/cm)
When H=100 km, the value of L' is obtained for the above specific parameters as 196 km(=L'). When H=150 km, then, L'=265 km, and when we take the value as H=200 km then L'=329 km. These three values of L' show that the slope between the trough and ridge becomes steep when the value of L' is large. This shows that the coastline recedes much more when the value of H is larger. Then, it could be a case of set back of the coastline.
If we put the values of H=150 km and L'=265 km, then, the pattern of the model crustal upheaval might be taken to be similar to the pattern as seen in a part of the actual coastal area. That is, for example, as is noted by Nakamura (2001), for a meridional cross section of the crustal surface or the geographical land surface in the neighboring area covering the Nankai Trough and Kii Peninsula through Kushimoto.
LOADING EFFECT OF SEA LEVEL RISE TO CRUST
In a case of that considering for the relation between the vertical displacement w and the sea level rise in the ocean, it must be helpful to apply the above model.
Looking at the solution expressed as in (6) or (7), the maximum of the expected crustal upheaval is simply controlled by the factor [S0H0]. When the densities of the seawater and of the crust as a plate in the model are ρ0=1.03 and ρ=3.3, and the expected sea level rise is H0=125 m for the case of that the value of [S0H0] is 39 m.
When the value of H0 is increased, the locations of the trough and ridge in the model are unchanged, and the slope between the trough and ridge becomes steep. In this case, the location of the coastline would never change (Fig.2).
For some case with several possible factors affecting to the sea level rise, it can be considered that there is a threat of a set back of the coastline. Hence, we should be careful, in considering the related problems, to see the location of the coastline and to know the horizontal shifts of the trough and ridge. It is also necessary to consider the vertical displacement of the crustal surface.
Although this work may be helpful for our dynamical understanding of the crustal upheaval, the pattern of the crustal surface in the coastal zone should be studied more at any actual case with careful consideration of what parameters are more actively controlling the solution. In fact, any one of the existing plates on the earth has a boundary so that it might be more practical to introduce several additional factors for obtaining a more realistic solution of an advanced model. Now, it can be seen well that the solution in this work may give an essential suggestion to the actual process of the crustal upheaval in practice.
|