図1・15　直列共振回路

　

この理由は図1・11で示したようにコイルとコンデンサに流れる電流、i_Lとi_Cとがプラスとマイナスの逆向き(逆相)に流れて互いに打ち消し合い、合成リアクタンスがゼロとなることによる。このためにはコイルとコンデンサのリアクタンスの大きさが等しいことが必要であり(1・13)式と(1・16)式から

共振したときに流れる電流はコイルとコンデンサのリアクタンスX_LとX_Cが互いに打ち消すので抵抗Rだけの回路と等価となり直列共振回路の共振電流は

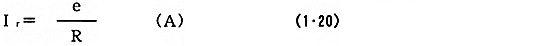
となる。ここで、eは回路に加える電圧、Rは抵抗分である。

共振回路による周波数選択性の良さはQで表され

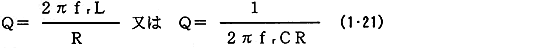
となり、抵抗Rが小さいほど、インダクタンスLが大きいほど、及び容量Cは逆に小さいほどQが大きくなり、鋭い同調特性が得られる。

前ページ　　　目次へ　　　次ページ