(式10)においてα=oとした場合、すなわち、電圧の位相が零の時短絡し、従って短絡電流が最大となって現れる場合の短絡後数サイクルの電流を交流分と直流分に分けて図示すると図2.15のようになる。
交流分と直流分を合成した短絡電流が最大値となるのは(式10)の右辺をtについて微分したものへα=oを代入した結果が零となる時間tの時である。
この時間tの値は発電機の諸定数(x"d、x′d、T"d、T′d及びTdc)の値によって決まるが、図16から明らかなように短絡後1/2サイクル、すなわち1/120秒(60Hzの場合)を越えるところには最大値は現れないことがわかる。
一方実際の発電機においては最大値は1/2サイクルに近いところに現れることもあるためかIECの計算方式においては短絡後1/2サイクルの時の値を最大値と見做している。
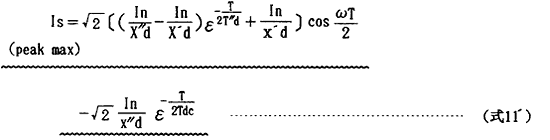
ただしTは1サイクルの時間である。
また(式11′)は発電機が無負荷時の式であるがIECではIs(peak max)の値については定格負荷時であっても、交流分実効値を求める時(式6)で行ったような、倍率を掛けることは行わないことにしている。
(b) 電動機の短絡電流
短絡電流の供給源は、先に述べた発電機のみならず短絡時に運転されていた電動機からも短絡電流は供給される。
IECではこの電動機から供給される短絡電流の計算に際しては、短絡時に同時に運転されていた総ての電動機の定格出力の合計に等しい定格出力を持ち、かつ、主母線に直接接続された1台の仮想電動機から短絡電流が供給されると考えてよいとしている。
この電動機からの短絡電流は持続短絡電流を供給することはなく非常に短時間で減衰してしまう。
また、この短絡電流は無負荷時が最大となり負荷時はそれよりも少い値となるため、IECでは仮想電動機からの短絡電流は総て無負荷時の値を用いることとしている。