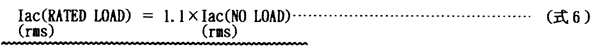
従って、IEC方式によって、実際に発電機の短絡電流の交流分実効値を計算する場合には(式6)にもとずいて定格負荷時の値を求めこの値を使用すべきである。
(ii) 直流分
これまで、発電機短絡電流の交流分についてのみ説明して来たが、短絡電流、特に短絡初期における短絡電流を論ずる場合には直流分が含まれることを考慮しなければならない。短絡回路にリアクタンスがある限り短絡電流の中には必ず直流分が含まれるが、その値は交流分と同じように短絡瞬時の電圧の位相によって異る。
短絡直後の短絡電流は交流分と直流分の合成となって熱的及び電磁力的に大きく作用し種々の障害を起すおそれがある。
短絡時の直流分の大きさは次の式で表すことが出来る。
ただし
Idc:発電機短絡電流直流分(A)
Ra:電機子巻線の抵抗(Ω)
X"q:横軸初期過渡リアクタンス(Ω)
Tdc:電機子時定数(秒)
一般にX"qはX"dとほぼ同じと考えてよいので(式7)は次のようになる。

(式8)における直流分の減衰時定数Tdcは一般には小さく数サイクル程度である。
また直流分短絡電流が負記号を持つのは電圧の位相が任意の値αの時に短絡した場合、短絡瞬時すなわちt=oにおいては、直流分は、(式3)によって求められた交流分とは必ず逆の極性をとることを意味する。
また、交流分の項で述べたように交流分は短絡瞬時すなわちt=oの時、電圧の位相が零又はπ(180°)の場合が最大となるが(式8)をよく見れば直流分も短絡瞬時の位相が零又はπ(180°)の場合が最大となることがわかる。