The advantage gained by using Boundary Element Method (BEM) [14] -based algorithm is the ability to readily accommodate the changes in the unknown boundary shape as it evolves from its initial to its final shape.
The present work addresses the developments of the conjugate gradient algorithms for estimating frost growth on an evaporating tube in transient heat conduction problem. The conjugate gradient method derives from the perturbation principles and transforms the inverse problem to the solution of three problems, namely, the direct, sensitivity and the adjoint problem. The method will be discussed in detail.
II. THE DIRECT PROBLEM
To illustrate the methodology for developing expressions for use in determining the frost growth on an evaporating tube, we consider the following two-dimensional inverse moving boundary heat conduction problem. Initially the system has temperature Ti along tube surface Γ1, when t>O, the frost may growth on the tube surface Γ1. The boundary conditions on the tube surface Γ1 and frost surface Γ2 are assumed both convective boundary conditions. Figure 1 shows the geometry and the coordinates for the two-dimensional physical problem considered here, where the dots "●" (M=9) and triangles "Δ" (M=5) denote the sensor locations on the tube surface Γ1.
The dimensionless mathematical formulation of this linear moving boundary heat conduction problem in determining the frost temperature is given as:

Let us use N constant elements over space domain and J constant elements over time domain. Based on these assumptions, the following discretized boundary integral equation is obtained
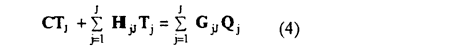
Where T = vector of temperature over N boundary elements at time j
Q = vector of the heat flux densities at time j
H,G = geometry and time dependent matrices of dimension (N, N)
C = diagonal matrix of dimension (N, N)
Transferring all unknowns to the left-hand side gives
AX = B (5)
where X is the vector of unknown T and q boundary values. B is found by multiplying the corresponding columns by the known values of T's or q's.
The computer program for this transient moving boundary heat conduction problem is modified based on the steady-state potential problem given in the text book by Brebbia and Dominguez [14] and the constant boundary elements over space and time are adopted for all the examples illustrated here.
The direct problem considered here is concerned with the determination of the medium temperature when the boundary geometry along Γ2(x,y,t), other thermal properties and the boundary conditions are known.
III THE INVERSE PROBLEM
For the inverse problem consider here, the boundary geometry (i.e, shape of the frost) along Γ2(x,y,t) is regarded as being unknown, but everything else in equation (1) are known. In addition, temperature readings taken at some appropriate locations and time on the tube are considered available.
Referring to Figure 1, we assumed that M sensors installed along Γ1 are used to record the temperature information to identify boundary configuration along Γ2(x,y,t) in the inverse calculations. Let the temperature reading taken within these sensors be denoted by Y(xm,ym,t) ≡ Ym(t), m = 1 to M, where M represents the number of thermocouples. We note that the measured temperature Ym(t) contains measurement errors. Then the inverse problem can be stated as follows: by utilizing the above mentioned measured temperature data Ym(t), estimate the unknown boundary configuration Γ2(x,y,t).
The solution of the present inverse problem is to be obtained in such a way that the following functional is minimized: