Fig. 1 Coupled vibration model
This vibration model gives the equation of motion as shown in Eq. (1). In the equation, the non-linear spring constant of gear backlash is represented by the dead zone, i.e., the transmitted torque is proportional to the relative angular displacement between the pinion and the wheel gear with dead zone. The oil film force is calculated based on the oil film theory of Gumbel.

The journal angular velocity is substituted with u ω in Eq. (1).
2.2 Characteristic equations
In order to look for the stable area of the simplified vibration model, the non-linear equations are made linear and the characteristic equations are used, in which it is assumed that gear backlash is negligibly small and that the wheel gear is large enough to be considered as fixed. And also it is assumed that oil film force is proportional to the relative velocity and displacement from the equilibrium point in the vicinity of the said point.
Linear spring constant and damping coefficient of the oil film are calculated from the non-dimensional coefficient dominated by the eccentricity ratio ε0 of the equilibrium point by means of the oil film theory of Gumbel as follows.

As a result, the characteristic equations are given as follows;
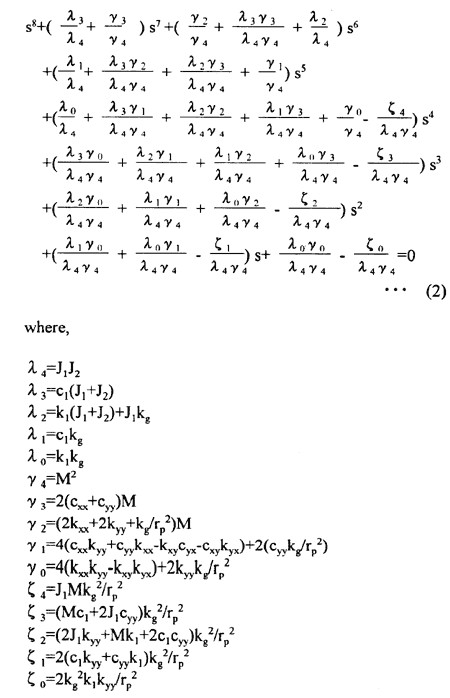
It is possible to obtain the stable area of the vibration model by the Hurwitz stability criterion applied for the said characteristic equation, but in this paper the stability is judged from the sign of the real part of the root of the characteristic equation, which is numerically solved.